Bài toán chi tiết
Bài 1002 (Đề thi Chuyên toán lớp 10 KHTN năm học 2023 - Vòng 2)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1576
BẢN INCho tam giác \(A B C\) nhọn với \(A B \lt A C\) nội tiếp trong đường tròn \((O)\) có tiếp tuyến tại \(A\) của \((O)\) cắt \(B C\) ở \(T\) sao cho \(T B>B C\). Gọi \(P\) và \(E\) lần lượt là trung điểm của \(T A\) và \(T C\).
1) Chứng minh rằng tứ giác \(A P E B\) nội tiếp.
2) Gọi giao điểm thứ hai của \(A E\) với \((O)\) là \(F\). Lấy \(G\) thuộc \((O)\) sao cho \(F G\) song song với \(A C\). Chứng minh rằng \(\widehat{A T G}=\widehat{T A F}\).
3) Gọi \(H\) là trực tâm của tam giác \(A B C, D\) là giao điểm của \(A H\) và \(B C . M\) là trung điểm \(B C\). K đối xứng với \(A\) qua \(B C\). \(N\) thuộc đường thẳng \(A M\) sao cho \(K N\) song song với \(H M\). Lấy \(S\) thuộc \(B C\) sao cho \(N S \perp N K\). Dựng \(R\) thuộc tia \(A K\) sao cho \(A R \cdot A H=A D^2\). \(Q\) là điểm sao cho \(P Q \perp A S\) và \(S Q \perp A O\). Chứng minh rằng điểm đối \(A R \cdot A H=A D \cdot Q\) uúng của \(A\) qua \(Q R\) thuộc đường tròn đường kính \(D N\). xứng của \(A\) qua \(Q R\) thuộc đường tròn đường kính \(D N\).
Cách giải 1
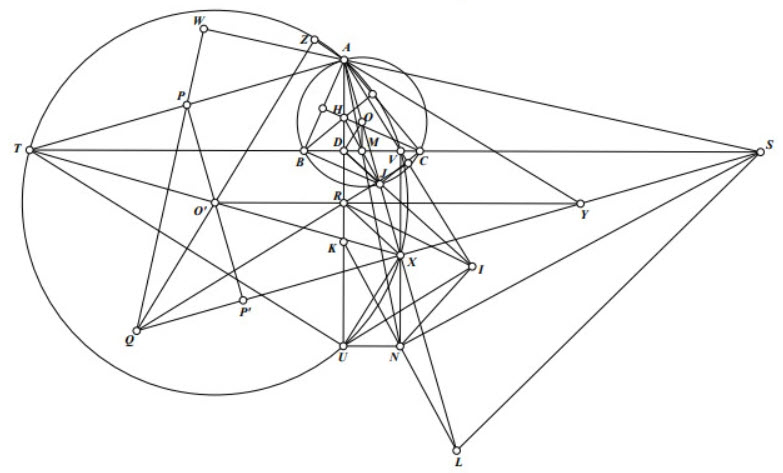
Gọi AJ là đường kính của \((\mathrm{O})\). Ta có BHCJ là hình bình hành nên M là trung điểm HJ . Gọi AJ cắt KN tại L . Do M là trung điểm HJ và \(\mathrm{HJ} / / \mathrm{KL}\) nên N là trung điểm KL . Mà \(\mathrm{NS} \perp \mathrm{NK}\) nên \(\mathrm{SL}=\mathrm{SK}\), mà \(\mathrm{SA}=\mathrm{SK}\) (do D là trung điểm AK ) nên \(\mathrm{SA}=\mathrm{SL}\).
Lại có: \(\mathrm{SQ} \perp \mathrm{AL}\) nên SQ là đường trung trực của AL hay SQ vuông góc AL tại trung điểm X của AL .
Gọi U đối xứng với A qua R. Ta có: \(A H \cdot A R=A D^2\) nên \(A H \cdot A U=A D \cdot A K\) \(\Rightarrow \dfrac{A M}{A N}=\dfrac{A H}{A K}=\dfrac{A D}{A U}\) nên \(\mathrm{DM} / / \mathrm{UN} \Rightarrow \mathrm{NU} \perp \mathrm{AU}\).
Ta có: NX//AK (đường trung bình) nên \(\mathrm{NX} / / \mathrm{OM}\), mà \(\mathrm{MD} / / \mathrm{NU}\) nên \(\dfrac{A O}{A X}=\dfrac{A M}{A N}=\dfrac{A D}{A U}\) nên OD//UX.
Ta có: \(A H . A U=2 A D^2\) nên \(\mathrm{OM} . \mathrm{AU}=\mathrm{AD}^2\)
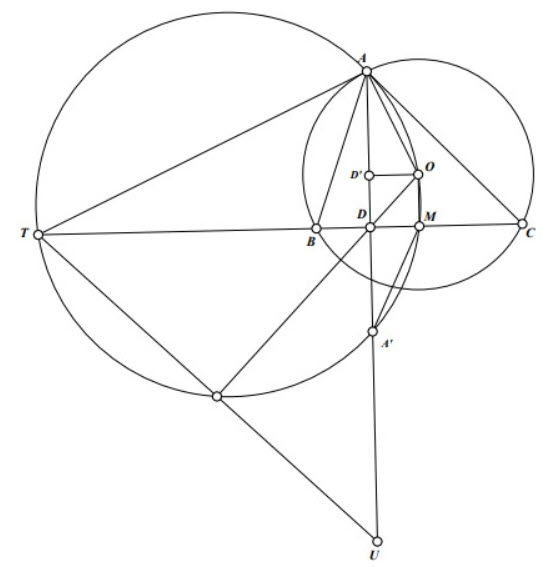
Ta có tứ giác OMTA nội tiếp \((\mathrm{OT})\). Gọi \((\mathrm{OT})\) cắt AD tại \(\mathrm{A}^{\prime}\). Có: AOMA ' là hình thang cân nên \(\mathrm{DA}^{\prime}-\mathrm{DA}^{\prime}=\mathrm{DA}^{\prime}-\mathrm{AD}^{\prime}=\mathrm{DD}^{\prime}=\mathrm{OM}\).
Do DT.DM=DA'.DA=DA.(DA-OM) \(=\mathrm{DA}^2\)-DA. \(\mathrm{OM}=\mathrm{OM} \cdot \mathrm{AU}-\mathrm{DA} \cdot \mathrm{OM}=\mathrm{OM} \cdot \mathrm{DU}\) \(\Rightarrow \dfrac{D T}{D U}=\dfrac{M O}{M D}\) nên \(\triangle \mathrm{DTU} \sim \Delta \mathrm{MOD}\) (c.g.c) \(\Rightarrow \angle \mathrm{DTU}=\angle \mathrm{DOM}\) nên \(\mathrm{OD} \perp \mathrm{TU}\).
Mà \(\mathrm{OD} / / \mathrm{UX}\) nên \(\angle \mathrm{TUX}=90^{\circ}\).
Ta có \(N X \perp B C\) tại \(V\) nên \(T, A, V, X, U\) thuộc \(\left(O^{\prime}\right)\) đường kính \(T X\).
\(\Rightarrow O^{\prime} R\) là đường trung trực của \(A U\) nên \(O^{\prime} R / / S T\) nên \(O^{\prime} R\) đi qua trung điểm \(Y\) của SX .
Gọi PO ' cắt QX tại \(\mathrm{P}^{\prime}\). Ta có: \(\mathrm{AT} / / \mathrm{XQ}\) mà \(\mathrm{O}^{\prime}\) là trung điểm TX nên \(\mathrm{O}^{\prime}\) là trung điểm \(\mathrm{PP}^{\prime}\). Ta cũng có: \(\mathrm{PO}^{\prime} / / \mathrm{AX}\) nên \(\mathrm{PP}{ }^{\prime} \perp \mathrm{XQ}\), mà \(\mathrm{PQ} \perp \mathrm{AS}\) nên \(\triangle \mathrm{P}^{\prime} \mathrm{PQ} \sim \triangle \mathrm{XSA}\) (g.g) mà \(\mathrm{O}^{\prime}, \mathrm{Y}\) là trung điểm PP ' và XS nên \(\triangle \mathrm{P}^{\prime} \mathrm{QO}^{\prime} \sim \triangle \mathrm{XAY}\) (c.g.c) nên \(\angle \mathrm{QO}^{\prime} \mathrm{P}^{\prime}=\angle \mathrm{XYA}\) nên \(\mathrm{QO}^{\prime} \perp \mathrm{AY}\) tại Z .
Suy ra YR.YO' \(=Y A . Y Z=Y X\). YQ nên tứ giác QO'RX nội tiếp.
Nên \(\angle \mathrm{O}^{\prime} \mathrm{RQ}=\angle \mathrm{O}^{\prime} \mathrm{XQ}=\angle \mathrm{XTA}=\angle \mathrm{XUA}=\angle \mathrm{VAU}\) (vì tứ giác AVXU nội tiếp và \(\mathrm{XV} / / \mathrm{AU}\) ). Mà \(\angle \mathrm{ARO}{ }^{\prime}=90^{\circ}\) nên \(\mathrm{QR} \perp \mathrm{AV}\).
Gọi I đối xứng với A qua QR thì \(\mathrm{QR} \perp \mathrm{AI}\) nên \(\mathrm{A}, \mathrm{V}, \mathrm{I}\) thẳng hàng.
Do \(\mathrm{RI}=\mathrm{RA}=\mathrm{RU}\) nên \(\angle \mathrm{AIU}=90^{\circ}\) dẫn đến \(\triangle \mathrm{ADV} \sim \Delta \mathrm{AIU}(\mathrm{g} . \mathrm{g})\)
\(\Rightarrow \dfrac{I A}{I U}=\dfrac{D A}{D V}=\dfrac{D A}{U N} \Rightarrow \dfrac{A D}{A I}=\dfrac{U N}{U I}\) mà \(\angle \mathrm{AUN}=\angle \mathrm{AIU}=90^{\circ}\) nên \(\angle \mathrm{IUN}=\angle \mathrm{IAU}\)
Từ đó \(\triangle \mathrm{ADI} \sim \Delta \mathrm{UNI}\) (c.g.c) \(\Rightarrow>\angle \mathrm{AID}=\angle \mathrm{UIN}=>\angle \mathrm{DIN}=\mathrm{AIU}=90^{\circ}\).