Toán 9 - Bất đẳng thức
Các bài toán chủ đề Toán 9 - Bất đẳng thức
Bài 2 (HSG lớp 10 – KHTN)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 879
Với \(a, b, c\) là các số thực dương thỏa mãn \(a + b + c = abc\). Chứng minh rằng:
\[ \sqrt{a^2 + b^2} + \sqrt{b^2 + c^2} + \sqrt{c^2 + a^2} + 3\sqrt{6} \leq \sqrt{8abc}. \]
Bài 3
| 1 cách giải | Unknow | Độ khó: 5 | Loại: Tự luận | Lượt xem: 824
Bài 4 (Revista Mathematica Timisoara)
| 2 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 831
Bài 5
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 794
Bài 6 (HSG 9, Quận Cầu Giấy, Hà Nội ngày 31/10/2024)
| 5 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 800
Bài 7 (Nguyễn Minh Thọ - HCM 09/11/2024)
| 1 cách giải | Unknow | Độ khó: 5 | Loại: Tự luận | Lượt xem: 815
Bài 8
| 0 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 246
Bài 9
| 0 cách giải | Unknow | Độ khó: 5 | Loại: Tự luận | Lượt xem: 234
Bài 10 (HSG 9 Vòng 2 - Quận Cầu Giấy, HN - 2024)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 803
Bài 11 (Russia MO 2004)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 907
Bài 12 (IMO Shortlist 1998)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 855
Bài 13 (APMO 1998)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 887
Bài 15 (Bài T5/569 - Tạp chí Toán học và tuổi trẻ)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 835
Bài 16 (Bài T5/565 Tạp chí Toán học và tuổi trẻ)
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 827
Bài 18 (Bài T9/565 Tạp chí toán học tuổi trẻ)
| 3 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 835
Bài 19 (Bài 7 (257 + 258) Tạp chí Toán tuổi thơ)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 834
Bài 20 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 828
Bài 21 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 839
Bài 22 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 816
Bài 23 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 827
Bài 24 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 815
Bài 25 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 843
Bài 26 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 848
Bài 27 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 801
Bài 28 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 820
Bài 29 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 823
Bài 30 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 848
Bài 31 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 845
Bài 32 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 835
Bài 33 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 820
Bài 34 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 810
Bài 35 (Trích đề thi HSG cấp tỉnh lớp 9 tỉnh Nghệ An năm học 2010 - 2011)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 836
Bài 36 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 874
Bài 37 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 824
Bài 38 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 822
Bài 39 (Tạp chí Toán học và tuổi trẻ số 564 tháng 06/2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 850
Bài 40 (Konstantinos Geronikolas, 22-11-2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 853
Bài 45 (Đề thi HSG Bắc Ninh 2024-2025 Tham khảo)
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 823
Bài 46
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 860
Bài 47
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 849
Bài 48
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 886
Bài 49
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 871
Bài 50
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 845
Bài 51
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 210
Bài 52
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 208
Bài 53
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 230
Bài 54
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 216
Bài 55
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 241
Bài 56
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 225
Bài 57
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 215
Bài 58
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 214
Bài 59
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 810
Bài 60
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 845
Bài 63 (Đề thi HSG toán 9 Hải Dương 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 229
Bài 64 (Đề thi HSG toán 9 Hải Dương 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 212
Bài 65 (Đề thi HSG toán 9 Hải Dương 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 230
Bài 66 (Đề thi HSG toán 9 Hải Dương 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 211
b) Gọi \(M\) là trung điểm của \(A B, M I\) cắt \(A C\) tại \(Q\). Xác định vị trí của điểm \(B\) trên tia đối của tia \(E A\) để chu vi của tam giác \(A M Q\) đạt giá trị nhỏ nhất.
Bài 67 (Đề thi HSG toán 9 Hải Dương 2024 - 2025)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 831
Bài 68 (Đề thi HSG toán 9 Hải Dương 2024 - 2025)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 802
Bài 71 (Đề chọn đội tuyển HSG Ba Đình 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 218
Bài 87 (Đề thi chọn Học sinh giỏi THCS Thành phố Lào Cai 2024 - 2025)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1820
1. Cho \(a, b\) là các số thực thỏa mãn \(a+b+a b=8\). Tìm giá trị nhỏ nhất của biểu thức \(P=a^2+b^2\).
2. Với \(a, b, c>0,3 b c-a c-a b=1\). Chứng minh rằng \(a^3 b^3 c^3+b^3+c^3 \geq 3 b^3 c^3\).
Bài 96 (Đề thi Học sinh giỏi lớp 9 Thành phố Huế 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 454
a) Chứng minh rằng với mọi số nguyên \(n\) chẵn thì \(n^3 + 20n + 96\) chia hết cho 48.
b) Cho ba số dương \(x, y, z\) thỏa mãn \(x + y + z = 6\). Chứng minh rằng: \[ \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \geq \frac{4}{9}z. \]
Bài 99 (Thi tuyển sinh vào lớp 10 năm học 2022-2023 của tỉnh Thái Bình)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 823
Cho các số dương \(a, b, c\) thay đối và thóa mãn \(a+b+c=2022\). Tìm giá trị nhỏ nhất của biểu thức
\[ \begin{aligned} M=\sqrt{2 a^2+a b+2 b^2} & +\sqrt{2 b^2+b c+2 c^2} \\ & +\sqrt{2 c^2+c a+2 a^2} . \end{aligned} \]
Bài 100 (Thi tuyển sinh vào lớp 10 năm học 2022-2023 của tỉnh Bắc Ninh)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 809
Cho các số thực \(a, b, c\) sao cho phương trình \(a x^2+b x+c+2022=0\) nhận \(x=1\) là nghiệm. Tìm giá trị nhỏ nhất của biểu thức
\[ \begin{aligned} & P=\sqrt{3 a^2-2 a b+3 b^2}+\sqrt{5 b^2-6 b c+5 c^2} \\ &+\sqrt{6 c^2-8 c a+6 a^2} \end{aligned} \]
Bài 101 (Thi thử vào lớp 10, THPT chuyên Hạ Long, Quảng Ninh, năm 2019)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 813
Cho \(x, y\) là càc số dương thỏa mãn \(x+y+z=\sqrt{2}\). Chứng minh
\[ \begin{aligned} & \sqrt{2019 x^2+2 x y+2019 y^2}+\sqrt{2019 y^2+2 y z+2019 z^2} \\ &+\sqrt{2019 z^2+2 z x+2019 x^2} \geq 2 \sqrt{2020} . \end{aligned} \]
Bài 102 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 816
Cho ba số thực dương \(a, b, c\) và \(k \geq 1\). Chứng minh rằng
\[ \frac{\sqrt{a^2-a b+b^2}}{a+b+k c}+\frac{\sqrt{b^2-b c+c^2}}{b+c+k a}+\frac{\sqrt{c^2-c a+a^2}}{c+a+k b} \geq \frac{3}{2+k}\]
Bài 103 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 840
Cho \(a, b, c\) là ba số thực dương thỏa mãn
\[ \frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a} \geq \frac{3}{2} \]
Chứng minh rằng
\[ \begin{aligned} & \frac{b}{\sqrt{3 a^2-4 a b+3 b^2}}+\frac{c}{\sqrt{3 b^2-4 b c+3 c^2}} \\ &+\frac{a}{\sqrt{3 c^2-4 c a+3 a^2}} \end{aligned} \]
Bài 104 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 822
Cho \(a, b, c\) là ba số thực dương. Chứng minh rằng
\[ \begin{aligned} & \sqrt{\frac{a b}{\sqrt{\left(b^2+b c+c^2\right)\left(c^2-c a+a^2\right)}}} \\ & \quad+\sqrt{\frac{b c}{\sqrt{\left(c^2+c a+a^2\right)\left(a^2-a b+b^2\right)}}} \\ & \quad+\sqrt{\frac{c a}{\sqrt{\left(a^2+a b+b^2\right)\left(b^2-b c+c^2\right)}}} \leq \sqrt[4]{27} . \end{aligned} \]
Bài 105 (Tạp chí Toán học và tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 824
Cho \(a, b, c\) là các số thực dương. Chứng minh rằng
\[ \frac{a^2}{a^2+3 a b+2 b^2}+\frac{b^2}{b^2+3 b c+2 c^2}+\frac{c^2}{c^2+3 c a+2 a^2} \geq \frac{1}{2} \]
Bài 106 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 800
Cho \(a, b, c\) là các số thực dương. Chứng minh rằng
\[ \frac{a^2}{a^2+3 a b+2 b^2}+\frac{b^2}{b^2+3 b c+2 c^2}+\frac{c^2}{c^2+3 c a+2 a^2} \geq \frac{1}{2} \]
Bài 107 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 812
Cho \(a, b, c\) là ba số thực dương. Chứng minh rằng:
\[ \frac{a^3}{4 a^2 b+4 a b^2+b^3}+\frac{b^3}{4 b^2 c+4 b c^2+c^3} +\frac{c^3}{4 c^2 a+4 c a^2+a^3} \geq \frac{1}{3} \]
Bài 108 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 829
Cho \(a, b, c\) là ba số thực dương. Chứng minh rằng
\[ \frac{a}{\sqrt{3 a^{2}-4 a b+3 b^{2}}}+\frac{b}{\sqrt{3 b^{2}-4 b c+3 c^{2}}} +\frac{c}{\sqrt{3 c^{2}-4 c a+3 a^{2}}}<2 \sqrt{2} \]
Bài 109 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 777
Cho \(a, b, c\) là ba số thực dương. Chứng minh rằng:
\[ \begin{aligned} \frac{a^{2}}{2 a^{2}+7 a b+2 b^{2}}+\frac{b^{2}}{2 b^{2}+7 b c+2 c^{2}} \\ +\frac{c^{2}}{2 c^{2}+7 c a+2 a^{2}} \geq \frac{3}{11} \end{aligned} \]
Bài 110 (Tạp chí TH &TT bài số 6 tháng 11/2023)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 856
Cho \(a, b, c\) là các số thực dương. Chứng minh rằng:
\[ \begin{aligned} \frac{a^{5}}{b^{2} \sqrt{\left(a^{2}+3 a b+b^{2}\right)^{3}}} & +\frac{b^{5}}{c^{2} \sqrt{\left(b^{2}+3 b c+c^{2}\right)^{3}}} \\ & +\frac{c^{5}}{a^{2} \sqrt{\left(c^{2}+3 c a+a^{2}\right)^{3}}} \end{aligned} \frac{3}{5 \sqrt{5}} \]
Bài 111 (Tạp chí Toán học tuổi trẻ số 567 tháng 9 năm 2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 825
Cho \(a, b, c\) là ba số thực dương và \(0<2 k<1\). Chứng minh rằng:
\[ \begin{gathered} \frac{a^{5}}{b^{2} \sqrt{\left(k a^{2}+t a b+k b^{2}\right)^{3}}}+\frac{b^{5}}{c^{2} \sqrt{\left(k b^{2}+t b c+k c^{2}\right)}} \\ +\frac{c^{3}}{a^{2} \sqrt{\left(k c^{2}+t c a+k a^{2}\right)^{3}}} \geq \frac{3}{(2 k+t) \sqrt{2 k+t}} . \end{gathered} \]
Bài 112
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 170
Cho ba số thực dương \(a, b, c\) thỏa mãn \(a^{4}+b^{4}+c^{4}=3\). Chứng minh rằng
\[ \begin{aligned} & \frac{a b}{\sqrt{3 a^{2}+2 a b+3 b^{2}}}+\frac{b c}{\sqrt{3 b^{2}+2 b c+3 c^{2}}} \\ &+\frac{c a}{\sqrt{3 c^{2}+2 c a+3 a^{2}}} \end{aligned} \frac{3}{8} \]
Bài 113
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 192
Cho ba số thực dương \(a, b, c\) thỏa mãn \(a^{4}+b^{4}+c^{4}=3\). Chứng minh rằng
\[ \frac{a b}{\sqrt{a^{2}-a b+b^{2}}}+\frac{b c}{\sqrt{b^{2}-b c+c^{2}}}+\frac{c a}{\sqrt{c^{2}-c a+a^{2}}} \leq 3 \]
Bài 114
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 204
Cho ba số thực dương \(a, b, c\) thỏa mãn \(a^{4}+b^{4}+c^{4}=3\). Chứng minh rằng
\[ \begin{aligned} & \frac{a b}{\sqrt{2 a^{2}-3 a b+2 b^{2}}}+\frac{b c}{\sqrt{2 b^{2}-3 b c+2 c^{2}}} \\ &+\frac{c a}{\sqrt{2 c^{2}-3 c a+2 a^{2}}} \end{aligned} \]
Bài 115
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 168
Cho ba số thực dương \(a, b, c\) thỏa mãn \(a^{3}+b^{3}+c^{3}=3\). Chứng minh rằng
\[ \begin{aligned} \frac{a b}{\sqrt{2 a^{2}+3 a b+2 b^{2}}}+ & \frac{b c}{\sqrt{2 b^{2}+3 b c+2 c^{2}}} \\ & +\frac{c a}{\sqrt{2 c^{2}+3 c a+2 a^{2}}} \leq \frac{3}{\sqrt{7}} \end{aligned} \]
Bài 116
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 183
Cho \(a, b, c\) là ba số thực dương. Chứng minh rằng
\[ \begin{aligned} & \frac{a^{2}}{2 a^{2}+5 a b+2 b^{2}}+\frac{b^{2}}{2 b^{2}+5 b c+2 c^{2}} \\ &+\frac{c^{2}}{2 c^{2}+5 c a+2 a^{2}} \geq \frac{1}{3} \end{aligned} \]
Bài 117
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 198
Cho \(a, b, c, k, t\) là các số thực dương tùy ý thỏa mãn \(t \geq k\). Chứng minh rằng
\[ \begin{aligned} & \frac{a^{2}}{k a^{2}+t a b+k b^{2}}+\frac{b^{2}}{k b^{2}+t b c+k c^{2}} \\ &+\frac{c^{2}}{k c^{2}+t c a+k a^{2}} \geq \frac{3}{2 k+t} \end{aligned} \]
Bài 118
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 169
Cho \(a, b, c, t, k, r\) là các số thực dương tùy ý thỏa mãn \(t \geq k \geq r\). Chứng minh rằng
\[ \begin{aligned} \frac{a^{2}}{r a^{2}+t a b+k b^{2}}+ & \frac{b^{2}}{r b^{2}+t b c+k c^{2}} \\ & \quad+\frac{c^{2}}{r c^{2}+t c a+k a^{2}} \geq \frac{3}{r+t+k} \end{aligned} \]
Bài 119
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 206
Cho \(a, b, c\) là các số thực dương. Chứng minh rằng
\[ \frac{a^{5}}{b^{2} \sqrt{\left(a^{2}+5 a b+b^{2}\right)^{3}}}+\frac{b^{5}}{c^{2} \sqrt{\left(b^{2}+5 b c+c^{2}\right)^{3}}} +\frac{c^{5}}{a^{2} \sqrt{\left(c^{2}+5 c a+a^{2}\right)^{3}}} \geq \frac{3}{7 \sqrt{7}} \]
Bài 124 (Bài P865 (Mức B) Tạp chí Pi số 12 năm 2024)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 193
Cho các số thực không âm \(a, b, c\) thỏa mãn \(a+b+c=4\). Chứng minh rằng
\[ \sqrt{2 a+\frac{(b-c)^2}{8}}+\sqrt{b}+\sqrt{c} \leq 4 \]
Bài 126 (Bài P867 (Mức A) Tạp chí Pi số 12 năm 2024)
| 0 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 189
Xét dãy số \(\left(x_n\right)\) xác định bởi
\[ x_1=\frac{3}{2}\]
và
\[ x_{n+1}=1+x_n-\frac{1}{2} x_n^2\]
với mọi \(n \geq 1\). Tìm tất cả các số thực \(a\) sao cho bất đẳng thức
\[ \sum_{k=1}^n \sqrt{x^2+x_k^2} \geq n \sqrt{x^2+a} \]
đúng với mọi số thực \(x\) và mọi số nguyên dương \(n\).
Bài 137 (Đề thi Học sinh giỏi Toán 9 tỉnh Nghệ An 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 209
Từ một tấm nhôm hình chữ nhật có kích thước \(5 dm, 8 dm\) (bề dày không đáng kể). Người ta cắt bỏ bốn hình vuông ở bốn góc, mồi hình vuông bị cắt bỏ có độ đại cạnh là \(a dm\) (phần tô đậm là phần bị cắt bô) rồi gập lại đề được một hình hộp chữ nhật không có nắp (xem hình vê bên). Giá thị trường của loai hình hộp chữ nhật này được bán dựa trên thể tich chứa của khối hộp với mức giá 20 nghìn đồng/ \(\mathrm{dm}^3\). Hỏi giá trị a bằng bao nhiêu để có thể bán hình hộp chữ nhật nói trên với mức giá cao nhất, hãy tinh mức giá cao nhất đó?
Bài 142 (Nguyễn Văn Hòa đề xuất)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 815
Cho \(a,b,c \geq 0\) thỏa mãn \(a^2+b^2+c^2=3\). Chứng minh rằng:
\[ \frac{a^2}{b} + \frac{b^2}{c} +\frac{c^2}{a} + abc \geq 4\]
Bài 143
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 786
Cho \(a,b,c\) là các số thực dương thỏa mãn \(a^2+b^2+c^2=3\). Chứng minh rằng:
\[ \frac{a^4}{1+bc} +\frac{b^4}{1+ca} +\frac{c^4}{1+ab} \geq \frac{a^2}{1+a^2} + \frac{b^2}{1+b^2} + \frac{c^2}{1+c^2} \]
Bài 144
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 804
Cho \(a,b,c\) là các số thực dương, chứng minh rằng:
\[ \frac{a^3}{b} + \frac{b^3}{c} + \frac{c^3}{a} +abc \geq 4\]
Bài 145 (Lê Thư)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 785
Cho \(a,b,c\) là các số thực không âm thỏa mãn \(a+b+c=3\). Chứng minh rằng:
\[ P = \frac{1}{\sqrt{3+a^2}} + \frac{1}{\sqrt{3+b^2}} + \frac{1}{\sqrt{3+c^2}} \leq \frac{3}{2} \]
Bài 146 (Konstantinos Geronikolas 12/2024)
| 4 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1800
Cho \(a,b,c\) là các số thực dương thỏa mãn \(a+b+c=3\). Chứng minh rằng:
\[ \frac{bc}{\sqrt{a^2+3}} + \frac{ca}{\sqrt{b^2+3}} + \frac{ab}{\sqrt{c^2+3}} \leq \frac{3}{2} \]
Bài 151 (Đề kiểm tra HK 1 Start Education chuyên toán 9 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1192
Cho \(a, b, c\) là các số không âm thỏa mān: \(a^2+b^2+c^2=3\). Chứng minh
a) \(a+b+c \leq 3 \leq a^3+b^3+c^3\)
b) \(\sqrt{2 a^4+6 b^2+6 c^2-13}+\sqrt{2 b^4+6 c^2+6 a^2-13}+\sqrt{2 c^4+6 a^2+6 b^2-13} \geq 3\)
Bài 175
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1819
Cho \(a, b \geq 0\). Chứng minh rằng
\[\left(a^{2}+b+\frac{3}{4}\right)\left(b^{2}+a+\frac{3}{4}\right) \geq\left(2 a+\frac{1}{2}\right)\left(2 b+\frac{1}{2}\right)\]
Bài 176
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1823
Cho các số dương \(x, y, z\) thỏa mãn \(x+y+z=1\). Chứng minh rằng
\[\frac{x}{x+\sqrt{x+y z}}+\frac{y}{y+\sqrt{y+z x}}+\frac{z}{z+\sqrt{z+x y}} \leq 1\]
Bài 177
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1826
Cho \(a, b, c>0\). Chứng minh rằng
\[\frac{a(b+c)}{\sqrt{b c\left(b^{2}+c^{2}\right)}}+\frac{b(c+a)}{\sqrt{c a\left(c^{2}+a^{2}\right)}}+\frac{c(a+b)}{\sqrt{a b\left(a^{2}+b^{2}\right)}} \geq 3 \sqrt{2}\]
Bài 178
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1825
Cho \(a, b, c>0\) thoả mãn \(a b c=1\). Chứng minh rằng
\[\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}+3 \geq 2(a+b+c)\]
Bài 179
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1785
Cho \(a \geq b \geq 1, a \leq 3, a b \leq 6, a b \leq 6 c\). Chứng minh rằng
\[a+b-c \leq 4\]
Bài 180
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1817
Cho \(a \geq b \geq 1, a \leq 3, a b \leq 6, a b \leq 6 c\). Chứng minh rằng
\[a+b-c \leq 4\]
Bài 181
| 3 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1838
Cho \(x, y, z>0\) thoả mãn \(x+y+z=1\). Tìm giá trị nhỏ nhất của
\[P=\frac{x^{2}(y+z)}{y z}+\frac{y^{2}(z+x)}{z x}+\frac{z^{2}(x+y)}{x y}\]
Bài 182
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1820
Bài 8. Cho \(a, b, c>0\) và \(a b+b c+c a=a+b+c\). Chứng minh rằng
\[\frac{a+b}{a^{2}+b^{2}}+\frac{b+c}{b^{2}+c^{2}}+\frac{c+a}{c^{2}+a^{2}} \leq 3\]
Bài 183
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1840
Bài 9. Cho các số thực \(a, b, c \in[0,1]\) thỏa mãn điều kiện \(a+b+c=2\). Tìm giá trị lớn nhất của biểu thức sau
\[P=\sqrt{a^{2}-4 a+5}+\sqrt{b^{2}-4 b+5}+\sqrt{c^{2}-4 c+5}\]
Bài 184
| 3 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1808
Cho \(a, b, c>0\) và \(a+b+c=a b c\). Chứng minh rằng
\[\frac{a}{b^{3}}+\frac{b}{c^{3}}+\frac{c}{a^{3}} \geq 1\]
Bài 185
| 3 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1824
Khi hệ \(\left\{\begin{array}{l}x^{2}+x y+y^{2}=3 \\ y^{2}+y z+z^{2}=16\end{array}\right.\) có nghiệm. Chứng minh rằng
\[x y+y z+z x \leq 8\]
Bài 186
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1857
Cho \(a, b, c>0\). Chứng minh rằng
\[\frac{a b^{2}}{c}+\frac{b c^{2}}{a}+\frac{c a^{2}}{b}+a^{2}+b^{2}+c^{2} \geq 2 \sqrt{\left(a b^{3}+b c^{3}+c a^{3}\right)\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)}\]
Bài 187
| 2 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1791
Cho \(x, y, z \in[0,1]\) thỏa mãn \(\dfrac{1}{4 x+5}+\dfrac{2}{4 y+5}+\dfrac{3}{4 z+5}=1\). Tìm giá trị lớn nhất của
\[P=x y^{2} z^{3}\]
Bài 188
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1858
Cho 4 số thực \(\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\) thỏa mãn: \(a b c d>a^{2}+b^{2}+c^{2}+d^{2}\). Chứng minh rằng
\[a b c d>a+b+c+d+8\]
Bài 189
| 4 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1819
Cho \(x, y, z\) là các số thực thỏa mãn \(x^{2}+y^{2}+z^{2}=3\). Tìm giá trị lớn nhất của
\[P=x y+y z+2 z x\]
Bài 190
| 3 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1846
Cho \(x, y, z>0\) và \(x y z=8\). Tìm giá trị lớn nhất của biểu thức
\[P=\frac{1}{2 x+y+6}+\frac{1}{2 y+z+6}+\frac{1}{2 z+x+6}\]
Bài 191
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1826
Cho \(x, y \neq 0, x y(x+y)=x^{2}+y^{2}-x y\). Tìm giá trị lớn nhất của
\[P=\frac{1}{x^{3}}+\frac{1}{y^{3}}\]
Bài 192
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1859
Cho \(a, b, c\) đôi một khác nhau và thuộc \([0 ; 2]\). Tìm giá trị nhỏ nhất của
\[P=\frac{1}{(a-b)^{2}}+\frac{1}{(b-c)^{2}}+\frac{1}{(c-a)^{2}}\]
Bài 193
| 3 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1868
Cho \(a, b, c\) là các số thực dương. Chứng minh rằng
\[\frac{a^{2}}{2 a^{2}+b c}+\frac{b^{2}}{2 b^{2}+a c}+\frac{c^{2}}{2 c^{2}+a b} \leq 1\]
Bài 194
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1832
Cho \(x, y \in \mathbb{R}\) thỏa mãn \(5 x^{2}+5 y^{2}-5 x-15 y+8 \leq 0\). Tìm giá trị nhỏ nhất của
\[S=x+3 y\]
Bài 195
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1830
Cho \(a, b, c>0\) thỏa mãn \(a b c+a+c=b\). Tìm giá trị lớn nhất của
\[P=\frac{2}{a^{2}+1}-\frac{2}{b^{2}+1}+\frac{3}{c^{2}+1}\]
Bài 196
| 3 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1833
Cho các số \(x, y, z\) thỏa mãn \(1 \leq x, y, z \leq 4\) và \(x \geq y, x \geq z\). Tìm GTNN của biểu thức
\[P=\frac{x}{2 x+3 y}+\frac{y}{y+z}+\frac{z}{x+z}\]
Bài 197
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1846
Cho \(x \geq y \geq z>0\). Chứng minh rằng
\[\frac{x^{2} y}{z}+\frac{y^{2} z}{x}+\frac{z^{2} x}{y} \geq x^{2}+y^{2}+z^{2}\]
Bài 198
| 3 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1827
Cho \(a, b, c>0\). Chứng minh rằng:
\[\frac{a^{2}+b c}{b+c}+\frac{b^{2}+c a}{c+a}+\frac{c^{2}+a b}{a+b} \geq a+b+c\]
Bài 199
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1811
Cho \(a, b, c\) là các số thực dương thỏa mãn \(a+b+c=1\). Chứng minh rằng
\[\sqrt{a^{2}+\frac{1}{a^{2}}}+\sqrt{b^{2}+\frac{1}{b^{2}}}+\sqrt{c^{2}+\frac{1}{c^{2}}} \geq \sqrt{82}\]
Bài 200
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1826
Cho các số dương \(x, y, z\) thỏa mãn \(x y z=1\). Chứng minh rằng
\[\frac{x^{4} y}{x^{2}+1}+\frac{y^{4} z}{y^{2}+1}+\frac{z^{4} x}{z^{2}+1} \geq \frac{3}{2}\]
Bài 232 (Đề thi HSG toán 9 Thanh Hóa 2024 - 2025)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1826
Cho \(x, y, z\) là các số thực dương thỏa mãn: \(x y z(x+y+z)=3\). Chứng minh rằng:
\[ x^2+y^2+z^2 \leq \frac{1}{243}\left(x^5-2 x+4\right)^2\left(y^5-2 y+4\right)^2\left(z^5-2 z+4\right)^2 \]
Bài 350 (Bài 6 - Số 259 tạp chí Toán tuổi thơ 08/2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1931
Với \(a, b, c\) là các số thực không âm, tìm giá trị nhỏ nhất của biểu thực
\[ P=\frac{1}{a^2+b^2}+\frac{1}{b^2+c^2}+\frac{1}{c^2+a^2}+\frac{4(a+b+c)}{25} \]
Bài 351 (Bài 7 - Số 259 tạp chí Toán tuổi thơ 12/2024)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1834
Bài \(7(259)\). Cho các số thực \(x, y, z\) thỏa mãn \(x y+y z+z x=x y z\). Chứng minh rằng
\[(x+y+z+1)^2+8 \geq 4 x y z\]
Bài 431 (Đề thi HSG toán 9 Ngô Quyền, Hải Phòng 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Trắc nghiệm 1 lựa chọn | Lượt xem: 1127
Cho biểu thức \(B=\sqrt{4 x-2 \sqrt{4 x-1}}+\sqrt{4 x+2 \sqrt{4 x-1}}\) với \(\dfrac{1}{4} \leq x \leq \dfrac{1}{2}\). Khẳng định đúng là:
\(B>2\)
\(B>1\)
\(B=1\)
\(B<2\)
Bài 853 (Đề thi HSG toán 9 Thái Bình 2024 - 2025)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1817
Cho ba số dương \(a, b, c\) thỏa mãn \(a+b+c=1\) và \(a+b>c ; a+c>b ; b+c>a\).
Tìm giá trị lớn nhất của biểu thức \(M=\dfrac{4}{a+b}+\dfrac{4}{b+c}+\dfrac{4}{c+a}+\dfrac{a}{2 b c}+\dfrac{b}{2 c a}+\dfrac{c}{2 a b}-\dfrac{1}{2 a b c}\).
Bài 857 (Nguyễn Văn Hòa)
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1798
Cho \(a, b, c\) là các số thực dương thỏa mãn \(a b c=1\). Chứng minh rằng:
\[\dfrac{1}{\sqrt{5+4a}}+\dfrac{1}{\sqrt{5+4b}}+\dfrac{1}{\sqrt{5+4c}} \leq 1\]
Bài 858 (Nguyễn Văn Hòa 19/12/2024)
| 0 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1000
Cho \(a, b, c, p, q\) là các số thực dương thỏa mãn \(a b c=1 ; p+q=9 ; \dfrac{p}{q} \geq 1\). Chứng minh rằng:
\[ \frac{1}{\sqrt{p+q a}}+\frac{1}{\sqrt{p+q b}}+\frac{1}{\sqrt{p+q c}} \leq 1 \]
Bài 863 (Đề thi vào 10 PTTH Chuyên toán Bắc Giang 2023 - 2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1840
Cho \(x, y, z\) là các số thực dương và thỏa mãn điều kiện \(x+y+z=x y z\).
Tìm giá trị lớn nhất của biểu thức
\[P=\dfrac{1}{\sqrt{1+x^2}}+\dfrac{1}{\sqrt{1+y^2}}+\dfrac{1}{\sqrt{1+z^2}} \]
Bài 866 (Đề thi vào 10 PTTH Chuyên toán Hà Nội 2023 - 2024)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 2705
1. Tìm tất cả cặp số nguyên \((x, y)\) sao cho \(x y\) là số chính phuơng và \(x^2+x y+y^2\) là số nguyên tố.
2. Với các số thực không âm \(a, b\) và \(c\) thỏa mãn \(a+2 b+3 c=1\), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
\[P=(a+6 b+6 c)(a+b+c)\]
Bài 870 (Đề thi thử HSG 9 lần 3 - Câu lạc bộ toán A1)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
a) Với \(x, y, z>0\) thỏa mãn \(x+y+z=x y+y z+z x\), tìm giá trị nhỏ nhất của biếu thức
\[P=\dfrac{x^3}{\sqrt{2\left(y^4+1\right)}}+\dfrac{y^3}{\sqrt{2\left(z^4+1\right)}}+\dfrac{z^3}{\sqrt{2\left(x^4+1\right)}}\]
b) Trong hệ thập phân, có bao nhiêu số tự nhiên \(n\) có 4 chữ số sao cho tổng các chữ số của \(n\) bằng tổng các chữ số của \(n+2007\).
Bài 883 (Đề thi thử HSG 9 lần 4 - Câu lạc bộ toán A1)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
a) Cho \(x,y,x\) là các số thực không âm và không đồng thời bằng 0. Đặt
\[P=\frac{x}{y+z}+2 \sqrt{\frac{y}{z+x}}+3\sqrt[3]{\frac{z}{x+y}}\]
Tìm giá trị nhỏ nhất của \(P\).
b) Ba bạn Lãm, Mạnh, Toàn mỗi bạn viết lên bảng một số tự nhiên nhỏ hơn 32. Tính xác suất để tích ba số được viết lên bảng chia hết cho 4 nhưng không chia hết cho 16.
Bài 888 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2015 - 2016)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho \(\mathrm{x}, \mathrm{y}, \mathrm{z}\) là ba số thực dương. Chứng minh:
\[ \dfrac{x^2}{\sqrt{8 x^2+3 y^2+14 x y}}+\dfrac{y^2}{\sqrt{8 y^2+3 z^2+14 y z}}+\dfrac{z^2}{\sqrt{8 z^2+3 x^2+14 z x}} \geq \dfrac{x+y+z}{5} \]
Bài 893 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2016 - 2017)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho \(\mathrm{a}, \mathrm{b}, \mathrm{c}>0\) và \(a+b+c \geq 9\). Tìm GTNN của
\[ A=2 \sqrt{a^2+\dfrac{b^2}{3}+\dfrac{c^2}{5}}+3 \sqrt{\dfrac{1}{a}+\dfrac{9}{b}+\dfrac{25}{c}}\]
Bài 898 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2017 - 2018)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho các số dương \(a, b, c\), chứng minh rằng
\[ \dfrac{a^4}{b^3(c+2 a)}+\dfrac{b^4}{c^3(a+2 b)}+\dfrac{c^4}{a^3(b+2 c)} \geq 1 \]
Bài 903 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2018 - 2019)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho ba số dương \(\mathrm{a}, \mathrm{b}, \mathrm{c}\) thỏa mãn \(a b c=2\). Chứng minh rằng
\[ a^3+b^3+c^3 \geq a \sqrt{b+c}+b \sqrt{c+a}+c \sqrt{a+b} \]
Bài 908 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2019 - 2020)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho \(x, y, z\) là ba số thực dương thỏa mãn \(x(x-z)+y(y-z)=0\). Tìm giá trị nhỏ nhất cùa biểu thức
\[ P=\frac{x^3}{x^2+z^2}+\frac{y^3}{y^2+z^2}+\frac{x^2+y^2+4}{x+y} \]
Bài 913 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2020 - 2021)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho ba số dương \(x, y, z\) thỏa mãn \(x y+y z+z x=5\). Chứng minh
\[ \dfrac{x}{\sqrt{x^{2}+5}}+\dfrac{y}{\sqrt{y^{2}+5}}+\dfrac{3 z}{\sqrt{6\left(z^{2}+5\right)}} \leq \dfrac{2 \sqrt{6}}{3} \]
Đẳng thức xảy ra khi và chỉ khi nào?
Bài 918 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2021 - 2022)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho các số thực dương \(x, y, z\). Chứng minh rằng
\[ \frac{x \sqrt{x y}}{\sqrt{2 x+y}}+\frac{y \sqrt{y z}}{\sqrt{2 y+z}}+\frac{z \sqrt{z x}}{\sqrt{2 z+x}} \geq \sqrt{3 x y z} \]
Bài 923 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2022 - 2023)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho \(x, y, z>0\) thoả mãn \(3 x^{2} \leq 2\left(y^{2}+4 y z+z^{2}\right)\). Tìm giá trị nhỏ nhất của
\[ P=\dfrac{y^{2}}{\sqrt{3 x^{2}+20 x y+12 y^{2}}}+\dfrac{z^{2}}{\sqrt{3 x^{2}+20 x z+12 z^{2}}}+\dfrac{4}{(y+z)^{2}} \]
Bài 928 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2023 - 2024)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho các số thực \(a, b, c\) thoả mãn \(a+b+c=0\). Tìm giá trị nhỏ nhất của biểu thức:
\[ P=\dfrac{2 a-1}{a^{2}+2}+\dfrac{2 b-1}{b^{2}+2}+\dfrac{2 c-1}{c^{2}+2} \]
Bài 933 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho \(a, b, c\) là các số thực dương thỏa mãn \(a b c=1\). Tìm giá trị lớn nhất của biểu thức
\[ P=\dfrac{1}{a^3+b^2+c}+\dfrac{1}{b^3+c^2+a}+\dfrac{1}{c^3+a^2+b} \]
Bài 936 (Thi thử Chuyên KHTN năm học 2025 - 2026 (Vòng 1))
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 2119
1) Tim \(x, y\) nguyên thoả mãn
\[ x^3+2 y^3+2 x^2 y+y^2 x+x+2 y=3 \]
2) Với \(x, y, z\) là những số thực thoả mãn
\[ 0 \lt x \leq y \leq z \leq 3, \quad y+z \leq 5, \quad x+y+z \leq 6 \]
Chứng minh rằng
\[ x^2+y^2+z^2 \leq 14 \]
Bài 940 (Thi thử Chuyên KHTN năm học 2025 - 2026 (Vòng 2))
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 2065
1) Tìm \(x, y\) nguyên thỏa mān
\[ y=\dfrac{x+1}{x^4+1} \]
2) Với \(a, b, c\) là những số thực dương thỏa mãn \(a b+b c+c a=1\). Tìm giá trị nhỏ nhất của biểu thức
\[ P=2 a^2+b^2+c^2 \]
Bài 945 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 1)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
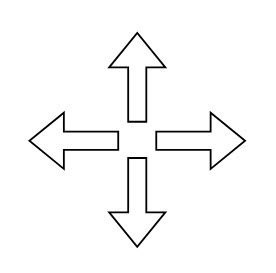
1. Bạn An chơi game trên máy tính điện tử, máy có phím di chuyển như hình bên. Mỗi lần nhấn phím di chuyển, nhân vật trong game sẽ di chuyển theo hướng mũi tên và độ dài mỗi bước đi là như nhau. Tính xác suất để sau bốn lần di chuyển, nhân vật trong game trở về đúng vị trí ban đầu.
2. Với các số thực \(a, b, c\) thỏa mãn: \(0 \leq a, b, c \leq 1\). Tìm giá trị lớn nhất của biểu thức:
\[ P=\dfrac{a}{\sqrt{2 b c+1}}+\dfrac{b}{\sqrt{2 c a+1}}+\dfrac{c}{\sqrt{2 a b+1}} \]
Bài 950 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 2)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
1) Cho \(x_1 ; x_2 ; \ldots ; x_{10}\) là các số nguyên dương thỏa mãn \(x_1+x_2+\ldots+x_{10}=100\). Tìm giá trị lớn nhất của biểu thức \(P=x_1 \cdot x_2+x_2 \cdot x_3+\ldots+x_9 \cdot x_{10}\).
2)
a) Tìm tất các số nguyên tố \(p, q, r\) thỏa mãn \(\dfrac{1}{p}+\dfrac{1}{q}+\dfrac{1}{r}+\dfrac{1}{p q r}=1\)
b) Tìm số tự nhiên \(n\) sao cho \(2^{2025}+2^{2022}+2^n\) là số chính phương.
Bài 958 (Đề thi Học sinh giỏi Toán 9 tỉnh Gia Lai năm học 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Cho \(a, b>0\) thỏa mãn \(\dfrac{1}{a}+\dfrac{1}{b}=6\). Tìm giá trị lớn nhất của biểu thức \(P=\dfrac{1}{3 a+6 b+1}+\dfrac{1}{6 a+3 b+1}\).
Bài 963 (Đề thi Học sinh giỏi Toán 9 tỉnh Lai Châu năm học 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
a) Cho \(x, y, z\) là các số dương thỏa mãn \(x+y+z=2025\). Tìm giá trị lớn nhất của biểu thức
\[ A=\dfrac{x}{x+\sqrt{2025 x+y z}}+\dfrac{y}{y+\sqrt{2025 y+z x}}+\dfrac{z}{z+\sqrt{2025 z+x y}}\]
b) Trên một măt bàn phẳng có 2025 đồng xu kích thước bằng nhau, mỗi đồng xu có hai mặt một mặt sấp và một mặt ngửa, đồng thời tất cả các đồng xu đều được xếp mặt ngửa. Trong giờ học ngoại khóa thầy giáo cho các em học sinh của trường thực hiện trò chơi "lật đồng xu" như sau: Mỗi lượt chơi phải đổi mặt 10 đồng xu nào đó trên mặt bàn. Hỏi sau 2026 lượt chơi có thể nhận đưọc tất cả 2025 đồng xu trên mặt bàn đều có mặt sấp hay không? Hãy giải thích vì sao?
Bài 966 (Thi thử Chuyên toán lớp 10 PTTH Lê Quý Đôn - Bà Rịa Vũng Tàu năm học 2025 - 2026)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
1) Chứng minh rằng với mọi số nguyên dương \(k\) và \(a\) là số nguyên tố lớn hơn 5 thì \(a^{4 k}-1\) luôn chia hết cho 240 .
2) Xét các số dương thay đồi \(a, b, c\). Tìm giá trị nhỏ nhất của biểu thức
\[ T=\dfrac{8\left(a^2+b^2+c^2\right)}{a b+b c+c a}+\dfrac{27(a+b)(b+c)(c+a)}{(a+b+c)^3} \]
Bài 970 (Thi thử Chuyên toán lớp 10 Phổ thông năng khiếu - TP. Hồ Chí Minh năm học 2025 - 2026 Vòng 2)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho ba số nguyên dương \(a, b, c\) thỏa mãn \(a^2+b^2+c^2=4 a b c-1\).
a) Chứng minh rằng \(a b c \geq 1\).
b) Chứng minh rằng \(a+b+c \geq \sqrt{a b c}+2\).
Bài 974
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1526
Cho 3 số thực \(a \geq b \geq c \geq 0\) thỏa mãn \(a + b + c \leq 1\). Chứng minh rằng:
\[ a^2 + 3b^2 + 5c^2 \leq 1\]
Bài 976 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 3)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
1) Một đơn vị bộ đội được xếp thành các hàng ngang. Nếu xếp mỗi hàng 3 người thì thừa 2 người, nếu xếp mỗi hàng 7 người thì thừa 4 người, còn nếu xếp mỗi hàng 5 người thì vừa đủ. Người chỉ huy không nhớ chính xác số quân của đơn vị, chỉ biết rằng số lượng nằm trong khoảng từ 500 đến 600 người. Hãy giúp người chỉ huy xác định chính xác số bộ đội của đơn vị.
2) Cho \(x, y\) là các số thực dương thỏa mān \(x>y>1\) và
\[ (x y+1)^2+(x+y)^2 \leq 2(x+y)\left(x^2-x y+y^2+1\right) . \]
Tìm giá trị nhỏ nhất của biểu thức
\[ P=\dfrac{\sqrt{x-y}}{y-1} \]
Bài 979 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 4 (Thi thử KHTN Vòng 2 - CLB Toán Lim))
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
1) Giải phương trình
\[ \dfrac{1}{x-1}+\dfrac{2}{x-2}+\dfrac{3}{x-3}+\dfrac{4}{x-4}=2 x^2-5 x-4 \]
2) Chứng minh rằng giá trị của biểu thức
\[ P=\dfrac{a-b}{a+b}+\dfrac{b-c}{b+c}+\dfrac{c-a}{c+a}+\dfrac{(a-b)(b-c)(c-a)}{(a+b)(b+c)(c+a)} \]
không phụ thuộc vào các số thực dương \(a, b, c\).
Bài 983 (Đề thi thử Chuyên toán lớp 10 ĐH Sư phạm năm học 2025 - Vòng 1)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
a/ Giải phương trình
\[ \sqrt{9-2 x^2}+\sqrt[3]{x^2+4}=3 \]
b) Cho \(x, y, z\) là các số thực dương thỏa mãn \(4 x^2+y^2=32 z^2\). Chứng minh rằng
\[ \dfrac{1}{x}+\dfrac{2}{y}-\dfrac{1}{z} \geq 0 \]
Bài 989 (Đề thi Chuyên toán lớp 10 KHTN năm học 2024 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1517
1) Tìm các số nguyên dương \(x, y, z\) thỏa mãn hệ phương trình
\[ \left\{\begin{array}{l} 27 x^3+27 x^2+10 y=(x+3 z)^3 \\ 27 y^3+27 y^2+10 x=(y+3 z)^3 \end{array}\right. \]
2) Với \(a, b, c\) là các số thực dương thỏa mãn điều kiện
\[ (a+2) b^2+(b+2) c^2+(c+2) a^2 \geq 8+a b c \]
Chứng minh rằng
\[ 2(a b+b c+c a) \leq a^2(a+b)+b^2(b+c)+c^2(c+a) \]
Bài 993 (Đề thi Chuyên toán lớp 10 KHTN năm học 2024 - Vòng 2)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 2062
a) Tất cả các số nguyên dương \(x, y\) thỏa mãn
\[ (x+y)^3+6 x y+3 y^2+y=8 x^3+9 x^2+1 \]
b) Xét các số thực dương \(x_1, x_2, \ldots, x_{2024}\) thỏa mãn \(x_1 x_2 \cdots x_{2024}=1\). Tìm giá trị nhỏ nhất của biểu thức
\[ P=\left(x_1^2-x_1+1\right)\left(x_2^2-x_2+1\right) \cdots\left(x_{2024}^2-x_{2024}+1\right) \]
Bài 997 (Đề thi Chuyên toán lớp 10 KHTN năm học 2023 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 2100
1) Giả sử \(n\) là số nguyên sao cho \(3 n^3-1011\) chia hết cho 1008 . Chứng minh rằng \(n-1\) chia hết cho 48.
2) Với \(a, b, c\) là các số dương thỏa mãn điều kiện \(a b+b c+c a=1\). Chứng minh rằng
\[ \left(1+\dfrac{1}{1+a^2}\right)\left(1+\dfrac{1}{1+b^2}\right)\left(1+\dfrac{1}{1+c^2}\right)>4 \]
Bài 1001 (Đề thi Chuyên toán lớp 10 KHTN năm học 2023 - Vòng 2)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 2092
1) Tìm tất cả các cặp số nguyên dương \((x ; y)\) thỏa mãn
\[ 4^x+\left(1+3^y\right)\left(1+7^y\right)=2^x\left(3^y+7^y+2\right) \]
2) Với \(x, y, z\) là những số thực dương, tìm giá trị nhỏ nhất của biểu thức:
\[ M=\dfrac{x^{14}-x^6+3}{x^2 y^2+z x+z y}+\dfrac{y^{14}-y^6+3}{y^2 z^2+x y+x z}+\dfrac{z^{14}-z^6+3}{z^2 x^2+y z+y x} \]
Bài 1007 (Đề thi Chuyên toán lớp 10 KHTN năm học 2022 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1531
Cho \(a, b, c\) là những số thực dương. Chứng minh rằng
\[ \dfrac{2 a}{a+b}+\dfrac{a+b}{a+c}+\dfrac{6 a+2 c}{3 b+c}+\dfrac{4 a+3 b+c}{b+c} \geq \dfrac{32 a}{2 a+b+c} \]
Bài 1009 (Đề thi Chuyên toán lớp 10 KHTN năm học 2022 - Vòng 2)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 2075
1) Tìm tất cả các cặp số nguyên dương \((x, y)\) thỏa mãn đẳng thức
\[ (x+y)(5 x+y)^3+x y^3=(5 x+y)^3+x^2 y^3+x y^4 \]
2) Với \(a, b, c\) là những số thực dương thỏa mãn các điều kiện sau:
\[ \left\{\begin{array}{cc} c \leq b<\mathrm{a} \leq 3, \quad b^2+2 a \leq 10, \quad b^2+2 a+2 c \leq 14, \\ \left(a^2+1\right)\left(b^2+1\right)+4 a b \leq 2 a^3+2 b^3+2 a+2 b . \end{array}\right. \]
Tìm giá trị lớn nhất của biểu thức
\[ P=4 a^2+b^4+2 b^2+4 c^2 \]
Bài 1012
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1508
Cho \(\mathrm{a}, \mathrm{b}, \mathrm{c}\) là các số thực không âm thỏa mãn \(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}=3\).
Chứng minh rằng
\[ \dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a} \geq \dfrac{5 \sqrt{3}}{6}\]
Bài 1016 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 5)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Cho \(x, y, z\) là các số thực không âm thỏa mãn \(x+y+z=3\). Tìm giá trị nhỏ nhất của biểu thức: \(P=x^2+y^2+2 z^2+2 x y z\).