Toán 9 - Hình học
Các bài toán chủ đề Toán 9 - Hình học
Bài 14
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 683
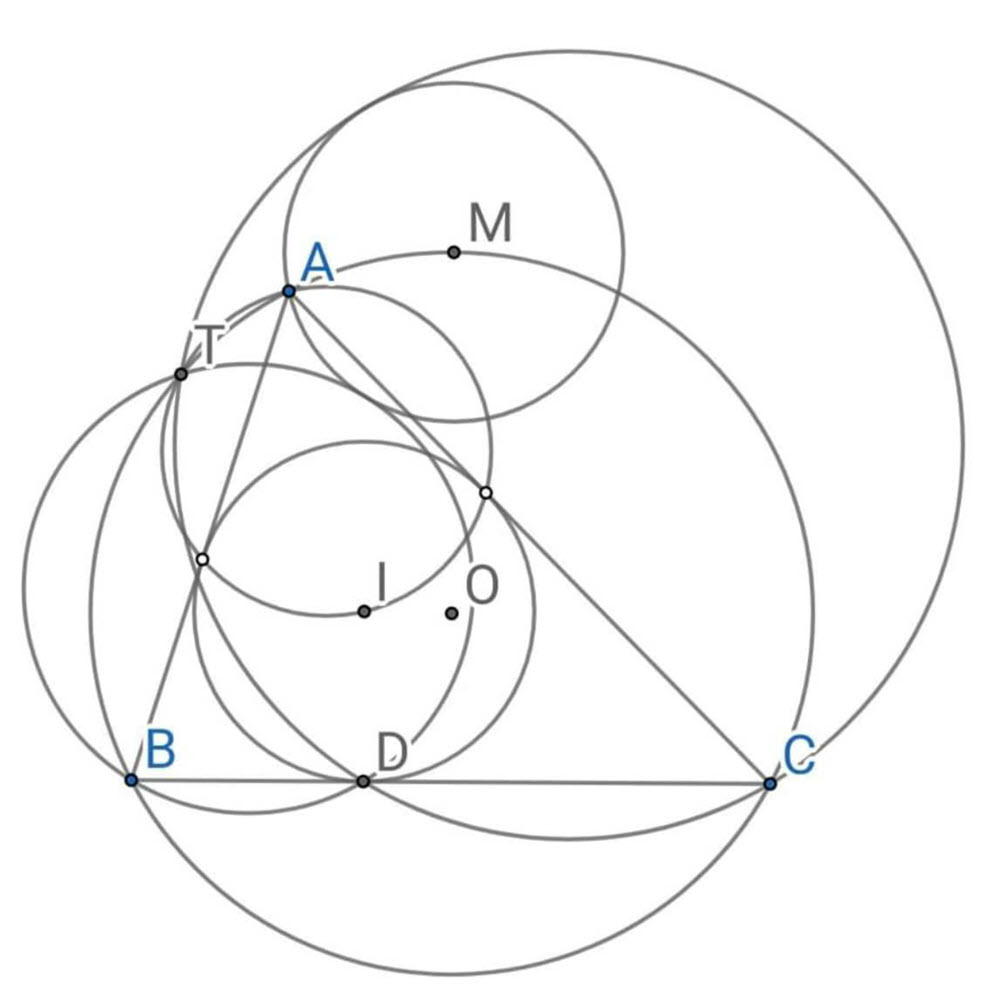
Bài 72 (Đề chọn đội tuyển HSG Ba Đình 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 162
a) Chứng minh \(\triangle A K O \backsim \triangle C G O\).
b) Gọi E F cắt O C tại S, A D cắt E F tại H. Chứng minh rằng \[ \frac{A K}{B K}=\frac{S E}{H E} \quad \text { và } \quad \frac{A K}{B K}=\frac{A E \cdot C E}{H E^2} . \] c) Dường thẳng qua E song song với C D cắt A D tại J. Trên tia đối của tia C A, lấy điểm L sao cho L J là phân giác \(\widehat{A L B}\). Gọi K L, A D cắt B E tại M, N. Chứng minh rằng B M=E N.
Bài 77 (Chọn học sinh giỏi THCS cấp tỉnh Khánh Hòa 2024 - 2025)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 653
a) Chứng minh \(\triangle A E F \backsim \triangle A B C\).
b ) Gọi \(I\) là trung điểm \(B C\), tia \(H I\) cắt \(B K\) tại \(N\). Chứng minh \(A N\) vuông góc \(E F\).
2) Cho góc nhọn \(\alpha\) biết \(\tan \alpha=2\). Tính giá trị biểu thức \[ M=\frac{\sin ^3 \alpha+\cos ^3 \alpha-\sin \alpha \cdot \cos ^2 \alpha}{4 \cdot \cos ^3 \alpha-3 \cdot \sin ^3 \alpha+8 \cdot \sin ^2 \alpha \cdot \cos \alpha} \]
Bài 81 (Chọn Học sinh giỏi lớp 9 tỉnh Ninh Bình)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 191
a) Chứng minh tứ giác OHMD nội tiếp.
b) Tiếp tuyến của (O) tại D cắt tia BC tại E , gọi N là trung điểm của MD . Chứng minh ba điểm ENO thẳng hàng.
c) Tiếp tuyến của (O) tại M cắt AB, AC lần lượt tại P và Q . Đường tròn (I) nội tiếp tam giác APQ tiếp xúc với AQ, PQ lần lượt tại D' và E'. Chứng minh rằng ba đường thẳng D'E', CM, AO đồng quy.
Bài 89 (Đề thi chọn Học sinh giỏi THCS Thành phố Lào Cai 2024 - 2025)
| 1 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1683
Cho tam giác \(ABC\) nhọn \((AB \gt AC\) nội tiếp đường tròn \((O)\), có đường cao \(AH\). Gọi \(I\) là tâm đường tròn nội tiếp tam giác \(ABC\). Đường thẳng \(AI\) cắt đường tròn \((O)\) tại điểm thứ hai là \(M\). Kẻ đường kính \(AK\) của đường tròn \((O)\). Đường thẳng \(MK\) cắt các đường thẳng \(AH\) và \(BC\) thứ tự tại \(P\) và \(Q\). Gọi \(F\) là giao điểm của \(AM\) và \(BC\).
a) Chứng minh: \(FA.FM=FH.FQ\).
b) Chứng minh: \(\triangle AKP\) cân.
c) Chứng minh: \(MB^2=MK . MQ\) và tứ giác \(QIHP\) nội tiếp.
d) Đường thẳng \(KI\) cắt đường tròn \((O)\) tại điểm thứ hai là \(D\). Hai đường thẳng \(AD\) và \(BC\) cắt nhau tại \(R\). Gọi \(E\) là trung điểm của \(AR\). Chứng minh ba điểm \(Q,I,E) thẳng hàng.
Bài 93 (Đề thi chọn HSG THCS tỉnh Quảng Bình 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 137
1) Hai con thuyền \(P\) và \(Q\) cách nhau 150 m và thẳng hàng với chân \(B\) của tháp hải đăng ở trên bờ biển. Từ \(P\) và \(Q\) người ta nhìn thấy đỉnh \(A\) của tháp hải đăng dưới các góc \(B P A=30^{\circ}\) và \(B Q A=60^{\circ}\) (tham khảo hình vẽ bên). Tính chiều cao \(A B\) của tháp hải đăng.
2) Cho nửa đường tròn \((O)\), đường kính \(A B\), lấy điểm \(C\) nằm trên nửa đường tròn \((O)\) ( \(C\) khác \(A\) và \(C\) khác \(B\) ). Gọi \(K\) là trung điểm của dây cung \(B C\). Qua \(B\) dựng tiếp tuyến với \((O)\) và cắt \(O K\) tại \(D\).
a) Chứng minh rằng \(A C\) song song với \(O K\).
b) Chứng minh rằng \(D C\) là tiếp tuyến \((O)\).
c) Vẽ \(C H \perp A B\) tại \(H\). Gọi \(I\) là trung điểm của \(C H\). Tiếp tuyến tại \(A\) của đường tròn \((O)\) cắt \(B I\) tại \(E\). Chứng minh rằng ba điểm \(E, C, D\) thẳng hàng.
Bài 98 (Đề thi Học sinh giỏi lớp 9 Thành phố Huế 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 126
Cho tam giác \(ABC\) nhọn có ba đường cao \(AD, BE, CF\) cắt nhau tại \(H\).
a) Chứng minh \(BH \cdot BE = BC \cdot BD\) và \(BH \cdot BE + CH \cdot CF = BC^2\).
b) Chứng minh \(BH = AC \cdot \cos \angle ABC\).
c) Gọi \(M, N, P, Q\) lần lượt là chân đường vuông góc từ \(H\) đến \(BE, CF, AB, AC\). Chứng minh 4 điểm \(M, N, P, Q\) thẳng hàng.
Bài 121 (Bài P862 (Mức B) Tạp chí Pi số 12 năm 2024)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 182
Cho tam giác không vuông \(A B C(A B<A C)\) với trực tâm \(H\), nội tiếp đường tròn \((O)\). Gọi \(L\) là đối xứng của \(A\) qua đường thẳng \(O H\). Chứng minh rằng tâm của đường tròn ngoại tiếp tam giác \(OHL\) nằm trên đường thẳng \(B C\).
Bài 139 (Đề thi Học sinh giỏi Toán 9 tỉnh Nghệ An 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 178
Cho đường tròn \((O)\) và dây cung \(B C\) cố định ( \(B C\) không đi qua tâm). Trên cung lớn \(B C\) lấy điểm \(A\) sao cho tam giác \(A B C\) nhọn và \( A B \lt AC \). Tiếp tuyến tại A của đường tròn \((O)\) cắt tiếp tuyến tại \(B\) và \(C\) của đường tròn \((O)\) tại điểm \(D\) và \(E\). Trên đường thằng \(B C\) lấy điểm \(K\) sao cho \(K E\) song song với \(B D\).
a) Chứng minh tam giác \(E A K\) cân.
b) Gọi \(H\) là trực tâm tam giác \(A B C\). Đường thẳng qua \(H\) cất các đường thẳng \(A B, A C\) lần lượt tại các điểm \(M, N\) sao cho \(H M=H N\). Chứng minh \(A H . H F=B F . N H\) với \(F\) là trung điểm \(B C\).
c) Gọi \(G\) là giao điểm của \(A B\) và \(O D\). Vẽ \(G I\) vuông góc với \(A C\) ( \(I\) thuộc \(A C\) ). Chứng minh rằng đường trung trực của đoạn thẳng \(IC\) luôn đi qua một điểm cố định khi \(A\) thay đổi.
Bài 150 (Đề kiểm tra HK 1 Start Education chuyên toán 9 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1121
Cho tam giác \(A B C\) nội tiếp đường tròn \((O, R)\) có các đường cao \(A D, B E, C F\) dồng quy tại trực tâm \(H\). Vẽ đường kính \(A L\). Cho biết \(\widehat{B A C}=60^{\circ}, \widehat{A C B}=45^{\circ}\).
a) Chứng minh tứ giác \(B H C L\) là hình bình hành và tính \(A H\) theo \(R\).
b) Gọi \(N\) là giao điểm của \(B E\) và \(O A\). Chứng minh rằng tứ giác \(B H O C\) nội tiếp và \(H\) là trung điểm của \(B N\).
c) Chứng minh rằng các đường thẳng \(C F, B O, D E\) đồng quy.
d) Gọi \(T\) là giao điểm của \(D E\) và \(O H\). Chứng minh rằng \(T F=T D\).
Bài 230 (Đề thi HSG toán 9 Thanh Hóa 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1104
Cho tam giác nhọn \(A B C\) nội tiếp đường tròn \((O)\), ba đường cao \(A D, B F, C E\) cắt nhau tại \(H\), vẽ \(O K \perp B C(K \in B C)\). Gọi \(I\) là trung điểm của \(A H\), gọi \(J\) là giao điểm của \(A H\) và \(E F\), kẻ đường kính \(A P\) của đường tròn \((O)\).
a. Chứng minh: \(O K=\frac{1}{2} A H\) và \(I K\) đi qua trung điểm của \(E F\).
b. Đường thẳng qua \(B\) song song với \(A C\) cắt đường thẳng \(C E\) tại \(S\). Chứng minh: \(I F^2=I J . I D\) và \(K S / / C J\).
Bài 231 (Đề thi HSG toán 9 Thanh Hóa 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1109
Cho tam giác \(A B C\) có ba cạnh tiếp xúc với đường tròn \((I)\). Gọi \(E, F\) lần lượt là tiếp điểm của đường tròn \((I)\) với \(A C\) và \(A B\). Gọi \(M, N\) lần lượt là trung điềm của \(B C\) và \(A C\). Chứng minh ba đường thẳng \(B I, M N, E F\) đồng quy.
Bài 854 (Đề thi HSG toán 9 Thái Bình 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1004
Cho tam giác \(A B C\) nhọn, các đường cao \(A D, B E, C F\) cắt nhau tại \(H\). Gọi \(M\) là trung điểm của HC, N là trung diểm của \(A C, A M\) cắt \(H N\) tại \(G\). Đường thắng đi qua \(M\) vuông góc với \(H C\) và đường thẳng đi qua \(N\) vuông góc với \(A C\) cắt nhau tại \(K\).
1) Chứng minh \(\triangle A B H\) đồng dạng \(\triangle M K N\) và tính \(\dfrac{G A^2+G B^2+G H^2}{G M^2+G K^2+G N^2}\).
2) Chứng minh \(3 \cos A+4 \cos B+6 \cos C<\dfrac{29}{4}\).
Bài 855 (Đề thi HSG toán 9 Thái Bình 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1004
Cho tam giác đều \(A B C\), đường tròn \((O)\) tiếp xúc với ba cạnh \(A B, A C, B C\) lần luợt tại ba điểm \(D,E,F\). Điểm \(M\) thuộc đường tròn \((O)\), tiếp tuyến tại \(M\) của đường tròn \((O)\) cắt các cạnh \(AB, AC\) theo thứ tự \(P,Q\) \((P \neq A, D ; Q \neq A, E)\).
1) Kẻ \(QH\) vuông góc với \(AP\) tại \(H\). Chứng minh: \(2.AH^2+2AH.PH=AP.AQ\) và tỉ số \(\dfrac{PQ^2+AP.AQ}{AP^2+AQ^2}\) không đổi
2) Chứng minh \(\dfrac{A P}{B P}=\dfrac{A P-A Q+C Q}{B P+C Q}\)
Bài 862 (Đề thi vào 10 PTTH Chuyên toán Bắc Giang 2023 - 2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1687
Cho đường tròn \((O ; R)\) và dây cung \(B C\) cố định của đường tròn thỏa mãn \(B C<2 R\). Một điểm \(A\) di chuyển trên \((O ; R)\) sao cho tam giác \(A B C\) có ba góc nhọn. Các đường cao \(A D, B E, C F\) của tam giác \(A B C\) cắt nhau tại \(H\). Đường phân giác của \(\widehat{C H E}\) kéo dài về hai phía cắt \(A B\) và \(A C\) lần lượt tại \(M\) và \(N\).
1. Chứng minh tam giác \(A M N\) cân tại \(A\).
2. Gọi \(I, P, Q, J\) lần luợt là hình chiếu của \(D\) trên các cạnh \(A B, B E, C F, A C\). Chứng minh rằng bốn điểm \(I, P, Q, J\) cùng nằm trên một đuờng thẳng vuông góc với \(A O\).
3. Đường tròn ngoại tiếp tam giác \(A M N\) cắt đường phân giác trong của \(\widehat{B A C}\) tại điểm thứ hai K. Chứng minh rằng HK luôn đi qua một điểm cố định.
Bài 867 (Đề thi vào 10 PTTH Chuyên toán Hà Nội 2023 - 2024)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1644
Cho tam giác \(A B C\) có ba góc nhọn \((A B \lt A C)\), nội tiếp đường tròn \((O)\). Ba đường cao \(A D, B E\) và \(C F\) của tam giác \(A B C\) cùng đi qua điểm \(H\). Đường thẳng \(E F\) cắt đurờng thẳng \(A D\) tại điểm \(Q\). Gọi \(M\) và \(I\) lần lượt là trung điểm của các đoạn thẳng \(B C\) và \(A H\). Đường thẳng \(I M\) cắt đường thẳng EF tại điểm \(K\).
1. Chứng minh tam giác \(AEK\) đồng dạng với tam giác \(A B M\).
2. Đường thẳng \(EF\) cắt đường thẳng \(B C\) tại điểm S, đường thẳng \(SI\) cắt đường thẳng \(M Q\) tại điểm \(T\). Chứng minh bốn điểm \(A, T, H\) và \(M\) cùng thuộc một đường tròn.
3. Tia \(TH\) cắt đường tròn \((O)\) tại điểm P. Chứng minh ba điểm \(A, K\) và \(P\) là ba điểm thẳng hàng.
Bài 872
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C\) nhọn, \(A B \lt A C\), nội tiếp đường tròn \((O)\), các đường cao \(B E, C F\).
a) Chứng minh \(A O \perp E F\).
b) Gọi tiếp tuyến tại \(A\) của \((O)\) cắt \(B C\) tại \(T\). Gọi \(N\) là trung điểm của \(A H\). Gọi đuờng thẳng \(T N\) cắt đường thẳng \(B E\) tại \(G\). Chứng minh \(A G \perp A B\).
c) Gọi đường thằng \(TN\) cắt cạnh \(AB,AC\) tại \(P,Q\). Điểm \(I\) thay đổi trên đoạn thẳng \(PQ\) (\(I\) khác \(P,Q\)). Điểm \(K, L\) thuộc đường thằng \(H Q, H P\) sao cho \(I K \perp A B, I L \perp A C\). Gọi \(P K\) cắt \(Q L\) tại \(S\). Kẻ \(D X\) vuông góc với đường thẳng \(IS\) tại \(X\). Chứng minh \(X\) thuộc một đường cố định khi \(I\) thay đổi.
Bài 882 (Đề thi thử HSG 9 lần 4 - Câu lạc bộ toán A1)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(ABC\) vuông tại \(A\) có \(M\) là trung điểm \(AB\). Gọi \(D\) là điểm trên đoạn thẳng \(BC\) sao cho \(BD=BA\) và \(P\) là điểm trên đường tròn ngoại tiếp tam giác \(ADC\) thỏa mãn \(\widehat{APB} = 90^o\).
a) Gọi \(U\) nằm trên đường thẳng \(AP\) sao cho \(BU\) vuông góc với \(MP\). Chứng minh rằng \(\widehat{BAP} = \widehat{UBP}\).
b) Gọi \(V\) là điểm nằm trên \(DP\) sao cho \(BV\) song song với \(MP\). Chứng minh rằng \(PU.BV = BU.PV\).
c) Chứng minh rằng đường thẳng \(CP\) chia đôi đoạn thẳng \(UV\).
Bài 887 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2015 - 2016)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tứ giác ABCD nội tiếp đường tròn O. Hai tia BA và CD cắt nhau tại \(K\). Hai tia AD và BC cắt nhau tại I . Gọi \(\mathrm{M}, \mathrm{N}\) lần lượt là trung điểm AC và BD . Các đường phân giác trong của các góc BKC và góc BLA cắt nhau tại I. Chứng minh:
a) \(\mathrm{DKL}+\mathrm{DLK}=\mathrm{ABC}\) và \(\mathrm{KIL}=90^{\circ}\)
b) \(\mathrm{KM} \cdot \mathrm{BD}=\mathrm{KN} . \mathrm{AC}\) và \(\mathrm{LM} \cdot \mathrm{BD}=\mathrm{LN} . \mathrm{AC}\)
c) Các đường phân giác trong của góc BKC, góc BLA và đường thẳng MN đồng quy
Bài 892
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C\) nhọn nội tiếp đường tròn tâm \(O\) có \(A B<A C\). Các đường cao \(B D, C E\) cắt nhau tại \(H\) ( \(D\) thuộc \(A C, E\) thuộc \(A B\) ). Gọi M là trung điểm của BC , tia MH cắt đường tròn \((\mathrm{O})\) tại N
a) Chứng minh rằng năm điểm \(\mathrm{A}, \mathrm{D}, \mathrm{H}, \mathrm{E}, \mathrm{N}\) cùng thuộc 1 đường tròn
b) Lấy điểm P trên đoạn BC sao cho \(\widehat{B H P}=\widehat{C H M}, \mathrm{Q}\) là hình chiếu vuông góc của A trên đường thẳng HP . Chứng minh rẳng tứ giác \(\operatorname{DENQ}\) là hình thang cân
c) Chứng minh rằng đường tròn ngoại tiếp tam giác MPQ tiếp xúc với đường tròn \((\mathrm{O})\)
Bài 897 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2017 - 2018)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C\) nhọn nội tiếp đường tròn \((O), Y\) trên cạnh \(C A, Z\) trên canh \(A B\) sao cho \(\widehat{A Z Y}>90^{\circ}\). Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(A Y Z, S\) là giao điểm khác \(A\) của \(A I\) và đường tròn \((O)\).
a) Chứng minh rằng \(\widehat{S A C}=\widehat{A Z Y}-90^{\circ}\).
b) Gọi \(X\) là giao điểm của \(Y Z\) và \(B C, M\) là giao điểm khác \(Y\) của các đường tròn ngoại tiếp tam giác \(A Y Z\) và \(C X Y\). Chứng minh rằng \(M\) nằm trên đường tròn \((O)\).
c) Gọi \(J, K\) là tâm các đường tròn ngoại tiếp tam giác \(B Z X\) và \(C X Y, T\) là giao điềm của \(A I\) và \(B J\). Chứng minh rằng 6 điểm \(T, O, M, I, J, K\) cùng nằm trên một đường tròn.
Bài 902 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2018 - 2019)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho đường tròn \((\mathrm{O})\) và một điểm A nằm bên ngoài đường tròn. Từ A kẻ các tiếp tuyến \(\mathrm{AB}, \mathrm{AC}\) với đường tròn \((\mathrm{B}, \mathrm{C}\) là các tiếp điểm). Đường thẳng AO cắt đường tròn \((\mathrm{O})\) tại hai điểm \(\mathrm{D}, \mathrm{E}(\mathrm{D}\) nằm giữa A và E\()\). Gọi H là giao điểm của BC và AO.
a) Chứng minh D là tâm đường tròn nội tiếp tam giác ABC .
b) Trên cung nhỏ CD của đường tròn \((\mathrm{O})\) lấy điểm F tùy ý ( F khác \(\mathrm{C}, \mathrm{D}\) ). Từ A kẻ đường thẳng vuông góc với lần lượt cắt \(\mathrm{FC}, \mathrm{FE}\) lần lượt tại \(\mathrm{M}, \mathrm{N}\).
Chứng minh rằng \(\dfrac{A B}{A E}=\dfrac{B D}{B E}\) và \(\dfrac{N F}{N E}=\dfrac{B D^2}{B E^2}\)
c) MB cắt \((\mathrm{O})\) tại \(\mathrm{P}(\mathrm{P}\) khá B\()\). chứng minh rằng NH song song với PD.
Bài 907 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2019 - 2020)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C\) nhọn nội tiếp đường tròn \((O)(A B<A C)\). Kẻ đường cao \(A H\) \((H \in B C)\) của tam giác \(A B C\) và kẻ đường kính \(A D\) của đường tròn \((O)\).
a) Gọi \(M\) là trung điểm của đoạn thẳng \(D H\). Chứng minh \(O M\) là đường trung trực của đoạn thẳng \(B C\).
b) Gọi \(S, T\) là các giao điểm của đường tròn \((O)\) với đường tròn tâm \(A\), bán kính \(A H ; F\) là giao điểm của \(S T\) và \(B C\). Từ \(A\) kẻ đường thẳng vuông góc với \(D H\) tại \(E\). Chứng minh \(F B \cdot F C=F H^2\) và ba điểm \(F, E, A\) thẳng hàng.
c) Chứng minh đường tròn ngoại tiếp tam giác \(B C M\) tiếp xúc với đường tròn tâm \(A\) bán kính \(A H\).
Bài 912 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2020 - 2021)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C\) vuông tại \(A(A B<A C), M\) là trung điểm cạnh \(B C\). \(P\) là một điểm di động trên đoạn \(A M\) ( \(P\) khác \(A\) và \(M)\). Đường tròn đi qua \(P\), tiếp xúc với đường thẳng \(A B\) tại \(A\), cắt đường thẳng \(B P\) tại \(K(K\) khác \(P)\). Đường tròn đi qua \(P\), tiếp xúc với đường thẳng \(A C\) tại \(A\), cắt đường thẳng \(C P\) tại \(L(L\) khác \(P)\).
a) Chứng minh \(B P . B K+C P . C L=B C^{2}\).
b) Chứng minh đường tròn ngoại tiếp tam giác \(P K C\) luôn đi qua hai điểm cố định.
c) Gọi \(J\) là tâm của đường tròn ngoại tiếp tam giác \(P K C\) và \(E\) là giao điểm thứ hai của đường tròn này với đường thẳng \(A C\). Gọi \(I\) là tâm của đường tròn ngoại tiếp tam giác \(P L B\) và \(F\) là giao điểm thứ hai của đường tròn này với đường thă้ng \(A B\). Chứng minh \(E F / / I J\).
Bài 917 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2021 - 2022)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác nhọn \(A B C \quad(A B \neq A C)\) nội tiếp đường tròn \((O)\). Gọi \(I\) là tâm đường tròn bàng tiếp trong góc \(\widehat{B A C}\) của tam giác \(A B C\). Đường thẳng \(A I\) cắt \(B C\) tại \(D\), cắt đường tròn \((O)\) tại \(E(E \neq A)\).
a) Chứng minh \(E\) là tâm đường tròn ngoại tiếp tam giác \(I B C\).
b) Kẻ \(I H\) vuông góc với \(B C\) tại \(H\). Đường thẳng \(E H\) cắt đường tròn \((O)\) tại \(F(F \neq E)\). Chứng minh \(A F \perp F I\).
c) Đường thẳng \(F D\) cắt đường tròn \((O)\) tại \(M(M \neq F)\), đường thẳng \(I M\) cắt đường tròn \((O)\) tại \(N(N \neq M)\). Đường thẳng qua \(O\) song song với \(F I\) cắt \(A I\) tại \(J\), đuờng thẳng qua \(J\) song song với \(A H\) cắt \(I H\) tại \(P\). Chứng minh ba điểm \(N, E, P\) thẳng hàng.
Bài 922 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2022 - 2023)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C\) cân \((A B=A C>B C)\) nội tiếp đuờng tròn \((O)\). Các đường phân giác trong \(B D, C E\) của tam giác \(A B C\) cắt nhau tại \(I, B I\) cắt \((O)\) tại \(F \neq B\). Điểm \(H\) đối xứng với \(C\) qua \(D\). Đường tròn ngoại tiếp tam giác \(H B C\) cắt \(B I\) tại \(K \neq B\).
a) Chứng minh rằng \(D C^{2}=D I . D B\) và \(D\) là trung điểm của đoạn thẳng \(I K\).
b) Kẻ \(K M\) song song với \(A C\) với \(M \in F C\). Chứng minh rằng \(M\) đối xứng với \(I\) qua \(A C\).
c) Gọi \(N\) là giao điểm của \(F C\) và \(A I, J\) là tâm của đuờng tròn ngoại tiếp tam giác \(I B E\). Chứng minh rằng \(M, N, J, D\) cùng nằm trên một đường tròn.
Bài 927 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2023 - 2024)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác nhọn \(A B C\) không cân nội tiếp đường tròn tâm \(O\). Vẽ đường kính \(A T\) của đường tròn \((O)\) và lấy điểm \(P\) trên đoạn thẳng \(O T(P \neq T)\). Gọi \(E\) và \(F\) tương ứng là hình chiếu vuông góc của \(P\) trên các đường thẳng \(A C\) và \(A B\). Gọi \(H\) là hình chiếu vuông góc của \(A\) trên cạnh \(B C\).
a) Chứng minh \(\widehat{O A B}=\widehat{H A C}\) và hai đường thẳng \(B C, E F\) song song với nhau.
b) Cho \(A H\) và \(E F\) cắt nhau tại \(U\); điểm \(Q\) di động trên đoạn thẳng \(U E(Q \neq U, Q \neq E)\). Đường thẳng vuông góc với \(A Q\) tại điểm \(Q\) cắt các đường thẳng \(P E, P F\) tương ứng tại \(M, N\). Gọi \(K\) là tâm đường tròn ngoại tiếp tam giác \(A M N\). Chứng minh bốn điểm \(A, M, N, P\) cùng thuộc một đường tròn và \(\widehat{O A H}=\widehat{K A Q}\).
c) Kẻ \(K D\) vuông góc với \(B C(D \in B C)\). Chứng minh đường thẳng đi qua điểm \(D\) và song song với \(A Q\) luôn đi qua một điểm cố định.
Bài 932 (Thi Chuyên toán Trần Phú - Hải Phòng năm học 2024 - 2025)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho đường tròn tâm \(O\), đường kính \(A B\). Vẽ đường thẳng \(d\) là tiếp tuyến tại điểm \(A\) của đường tròn \((O)\). Lấy điểm \(C\) cố định thuộc đoạn thẳng \(O A(C\) khác \(A\) và khác \(O\) ). Gọi \(D E\) là dây cung thay đổi của đường tròn \((O)\) nhưng luôn đi qua điểm \(C(D E\) khác \(A B)\). Các tia \(B D\) và \(B E\) cắt đường thẳng \(d\) theo thứ tự tại các điểm \(M\) và \(N\).
a) Chứng minh tứ giác \(D E N M\) là tứ giác nội tiếp đường tròn.
b) Gọi \(F\) là giao điểm thứ hai của đường tròn ngoại tiếp tam giác \(B M N\) và đường thẳng \(A B\). Chứng minh \(F\) là điểm cố định và tích \(A M \cdot A N\) không đổi khi dây cung \(D E\) của đường tròn \((O)\) thay dổi.
c) Gọi \(I\) là tâm đường tròn ngoại tiếp tứ giác \(D E N M\). Xác định vị trí của dây cung \(D E\) để tổng \(I B+I M\) đạt giá trị nhỏ nhất.
Bài 937 (Thi thử Chuyên KHTN năm học 2025 - 2026 (Vòng 1))
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1357
Với tứ giác \(A B C D\) lồi có hai đường chéo \(A C\) và \(B D\) cắt nhau tại \(P\). Giả sử \(Q\) là giao điểm thứ hai của các đường tròn ngoại tiếp các tam giác \(P A D\) và \(P B C\).
1) Chứng minh rằng hai tam giác \(Q D B\) và \(Q A C\) đồng dạng.
2) Chứng minh rằng \(2 \dfrac{A D}{B C} \leq \dfrac{Q D}{Q C}+\dfrac{Q A}{Q B}\).
3) Gọi \(M\) là trung diểm \(C D\). Giả sử \(Q\) nằm trong tam giác \(P C D\) và \(\angle Q P D=\angle M P C\). Chứng minh rằng \(A B C D\) là hình thang.
Bài 941 (Thi thử Chuyên KHTN năm học 2025 - 2026 (Vòng 2))
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1362
Cho hình thang \(A B C D\) nội tiếp đường tròn \((O)\) với \(A D || B C\) và \(A D \lt B C\). Giả sử tam giác \(A B C\) nhọn, không cân. Gọi \(P\) là điểm đối xứng của \(A\) qua \(B C\).
1) Chứng minh rằng \(D P\) đi qua trung điểm \(M\) của \(B C\).
2) Gọi \(K\) là trung điểm \(A P\). Chứng minh rằng \(K D\) đi qua trọng tâm tam giác \(A B C\).
3) Goi \(H\) là trực tâm tam giác \(A B C\). Giả sử có \(F\) nằm trên đường thẳng \(B D\) sao cho \(A F \perp H M\). Chứng minh rằng \(F K, A C, P D\) đồng quy.
Bài 946 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 1)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Cho tứ giác \(A B C D\) nội tiếp đường tròn \((O)\) với 2 đường chéo \(A C, B D\) vuông góc với nhau và không đi qua tâm. Trên đường tròn ngoại tiếp tam giác \(B O D\) lấy các điểm \(X, Y\) sao cho \(\widehat{A X O}=\widehat{C Y O}=90^{\circ}\). Gọi \(M\) là trung điềm của \(A C, T\) là giao điểm của \(A C, B D\), tia \(O T\) cắt đường tròn \(c_1\) ngoại tiếp tam giác \(B O D\) tại \(S\).
1. Chứng minh: \(O D^2=O T . O S\) và \(\widehat{X A T}=\widehat{X S T}\).
2. Chứng minh: \(B D\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(M X Y\).
Bài 952 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 2)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Tam giác nhọn \(A B C\) nội tiếp đường tròn \((O)\) có 3 đường cao \(A D, B E, C F\) cắt nhau tại \(H\). Dựng đường thẳng qua \(H\) cắt \(A B, A C\) lần lượt tại \(P, Q\) sao cho \(\triangle A P Q\) cân tại \(A\). Dựng đường kính \(A K\) của \((O)\). Đường phân giác trong của \(\widehat{B A C}\) cắt \(H K\) tại \(S\).
a) Chứng minh: \(B H C K\) là hình bình hành và hai tam giác \(\triangle A F H, \triangle A C K\) dồng dạng.
b) Chứng minh: \(H P\) là phân giác của \(\widehat{F H B}\).
c) Chứng minh: \(S\) nằm trên đường tròn ngoại tiếp tam giác \(A P Q\)
Bài 955 (Đề thi Học sinh giỏi Toán 9 tỉnh Gia Lai năm học 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Cho nừa đường tròn \((O ; R)\) đường kính \(A B\). Một điển \(M\) cố định thuộc đoạn thẳng \(O B\) ( \(M\) khác \(B\) và \(M\) khác \(O\) ). Đường thẳng \(d\) vuông góc \(A B\) tại \(M\) cắt nửa đường tròn đâ cho tại \(N\). Trên cung \(B N\) lấy \(E\) bất kì ( \(E\) khác \(B\) và \(E\) khác \(N\) ). Tia \(B E\) cắt đường thả̉ng \(d\) tại \(C\), đoạn thẳng \(A C\) cắt nưa đường tròn tại \(D\). Gọi \(H\) là giao điểm của \(A E\) và đường thẳng \(d\).
a) Gọi \(I\) là trung điểm của \(C H\), chứng minh rằng \(I D\) là tiếp tuyến của đường tròn \((0 ; R)\).
b) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác \(A H C\) di động trên một đường thẳng cố định.
Bài 962 (Đề thi Học sinh giỏi Toán 9 tỉnh Lai Châu năm học 2025)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Cho đường tròn \((O)\), dây \(C D\) cố đînh. Gọi \(B\) là điểm chính giữa cung nhỏ \(C D\), kẻ đường kính \(A B\) cắt \(C D\) tại \(I\). Lấy điểm \(H\) bất kỳ trên cung lớn \(C D, H B\) cắt \(C D\) tại \(E\). Đường thẳng \(A H\) cắt đường thẳng \(C D\) tại \(P\).
a) Chứng minh tứ giác PHIB nội tiếp.
b) Chứng minh \(A H \cdot A P=A I \cdot A B\).
c) Gọi \(K\) là giao điểm của đường thẳng \(A E\) và \(B P\). Kẻ \(K M \perp A B\) cắt \(A B\) tại \(M\), cắt đường tròn \((O)\) tại \(N\). Chứng minh \(N, I, H\) thẳng hàng.
Bài 967 (Thi thử Chuyên toán lớp 10 PTTH Lê Quý Đôn - Bà Rịa Vũng Tàu năm học 2025 - 2026)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác nhọn \(A B C(A B \lt A C)\) nội tiếp đường tròn \((O)\), đường cao \(A H\). Các tiếp tuyến tại \(B\) và \(C\) của đường tròn \((O)\) cắt nhau tại \(T\). Gọi \(D\) là giao điểm thứ hai của đường thẳng \(A T\) và đường tròn \((O) ; M\) là trung điểm của \(B C\).
1) Chứng minh ba điềm \(O, M, T\) thẳng hàng và \(\widehat{B A H}=\widehat{O C A}\).
2) Gọi \(K\) là hình chiếu vuông góc của \(O\) lên đường thẳng \(A T\). Chứng minh \(\triangle B K D\) đồng dạng với tam giác \(\triangle B A C\) và \(A B \cdot A C=2 A K . A M\).
3) Gọi \(P\) là hình chiếu vuông góc của \(O\) lên \(A M\). Chứng minh tứ giác \(H K P M\) là hình thang cân.
Bài 972 (Thi thử Chuyên toán lớp 10 Phổ thông năng khiếu - TP. Hồ Chí Minh năm học 2025 - 2026 Vòng 2)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C(A B /lt A C)\) nội tiếp dường tròn \((\mathrm{O})\). Kẻ các đường cao \(A D, B E(D \in B C, E \in A C)\), gọi \(H\) là trực tâm tam giác \(A B C\).
a) Gọi M là trung điểm của \(\mathrm{AH}, \mathrm{AD}\) cắt đường tròn \((\mathrm{O})\) tại F . Chứng minh \(\widehat{H E M}=\widehat{H F B}\).
b) Đường thẳng qua M song song BC và tiếp tuyến của \((\mathrm{O})\) tại A cắt nhau tại P. Chứng minh tứ giác \(A P D O\) nội tiếp.
c) Chứng minh \(P H \perp O F\).
Bài 977 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 3)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho hình bình hành \(A B C D\). Giả sử tồn tại hai điểm \(P\) và \(Q\) nằm trong hình bình hành \(A B C D\) sao cho hai tam giác \(A B P\) và \(B C Q\) đều là các tam giác đều.
1) Chứng minh rằng tam giác \(D P Q\) dều.
2) Gọi \(A Q\) cắt \(C P\) tại \(L\). Chứng minh rằng: \(L B=L Q+L C\).
3) Chứng minh rằng đường thẳng qua \(P\) vuông góc \(P D\) cắt đường thẳng qua \(Q\) vuông góc \(Q D\) cắt nhau tại một điểm nằm trên đường cao hạ từ \(B\) của tam giác \(A B C\).
Bài 981 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 4 (Thi thử KHTN Vòng 2 - CLB Toán Lim))
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác \(A B C\) nhọn ( \(A B \lt A C\) ) nội tiếp đường tròn \((O)\). Giả sử \(S\) là một diểm nằm trong tam giác \(A B C\) sao cho: \(\triangle S B A \backsim \triangle S A C\). Hình chiếu của \(A\) lên \(B C\) là \(D\).
1) Chứng minh rằng: \(B, S, O, C\) cùng thuộc một đường tròn.
2) Gọi \(M\) là trung diểm \(B C\). Chứng minh rằng: \(\angle S A B=\angle M A C\).
3) Gọi trung điểm \(C A, A B\) lần lượt là \(P, Q\). Chứng minh rằng: \(D S\) đi qua trung điểm \(P Q\).
Bài 987 (Đề thi thử Chuyên toán lớp 10 ĐH Sư phạm năm học 2025 - Vòng 1)
| 0 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác nhọn, không cân \(A B C\) nội tiếp đường tròn \((O)\), gọi \(A H, A D\) lần lượt là đường cao và đường phân giác trong góc \(A(H, D \in B C)\). Gọi \(M\) là giao điểm của \(A O\) và \(B C\). Đường trung trực của đoạn thẳng \(A D\) cắt \((O)\) tại \(E, F\). Chứng minh rằng
a) Trực tâm của tam giác \(D E F\) thuộc \((O)\).
b) Bốn điểm \(H, E, F, M\) cùng thuộc một đường tròn.
Bài 990 (Đề thi Chuyên toán lớp 10 KHTN năm học 2024 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1354
Cho hình vuông \(A B C D\). Lấy điểm \(P\) thuộc cạnh \(A B\) ( \(P\) khác \(A\) và \(B\) ). Gọi \(J\) là tâm đường tròn nội tiếp của tam giác \(P A D\).
1) Chứng minh rằng tứ giác \(P J D B\) nội tiếp.
2) Gọi \(H\) là trực tâm của tam giác \(P J D, S\) là giao điểm của \(J H\) và \(A D\). Chứng minh rằng \(S H=S D\).
3) Gọi \(L\) là tâm đường tròn nội tiếp của tam giác \(P B C, K\) là trực tâm của tam giác \(L P C\). Đường tròn nội tiếp của tam giác \(P C D\) tiếp xúc \(C D\) tại \(E\). Lấy \(F\) thuộc đoạn thẳng \(C D\) sao cho \(C F=D E\). Chứng minh rằng tam giác \(F H K\) vuông cân.
Bài 994 (Đề thi Chuyên toán lớp 10 KHTN năm học 2024 - Vòng 2)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1359
Cho tam giác \(A B C\) nhọn, không cân nội tiếp đường tròn \((O)\), có \(E, F\) lần lượt là trung điểm của các cạnh \(C A, A B\). Điểm \(P\) di chuyển trên cung nhỏ \(B C(P\) khác \(B, C)\). Gọi \(M, N\) lần lượt là giao điểm của các đường thẳng \(P C, P B\) với đường thẳng \(E F\). Các đường thẳng \(A M, A N\) cắt đường tròn \((O)\) theo thứ tự tại \(Q, R(Q, R\) khác \(A)\).
a) Chứng minh rằng tứ giác \(A F P M\) nội tiếp và \(\angle E P F=\angle Q P R\).
b) Chứng minh rằng giao điểm của hai đường thẳng \(Q E\) và \(R F\) nằm trên đường tròn \((O)\).
c) Lấy các điểm \(S, T\) lần lượt thuộc các đường thẳng \(C A, A B\) sao cho ba đường thẳng \(E T, F S, A P\) song song với nhau. Gọi \(K\) và \(L\) lần lượt là tâm đường tròn ngoại tiếp của các tam giác \(N F S\) và \(M E T\). Đường thẳng qua điểm \(K\) vuông góc với đường thẳng \(A B\) cắt đường thẳng qua điểm \(L\) vuông góc với đường thẳng \(A C\) tại điểm \(J\). Chứng minh rằng điểm \(J\) luôn nằm trên một đường thẳng cố định khi điểm \(P\) thay đổi.
Bài 998 (Đề thi Chuyên toán lớp 10 KHTN năm học 2023 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 1354
Cho hai đường tròn \((O)\) và \(\left(O^{\prime}\right)\) cố định cắt nhau tại \(A\) và \(B\) sao cho \(O\) nằm ngoài \(\left(O^{\prime}\right)\) và \(O^{\prime}\) nằm ngoài \((O)\). Trên đường tròn \((O)\) lấy điểm \(P\) di chuyển sao cho \(P\) nằm trong đường tròn \(\left(O^{\prime}\right)\). Đường thẳng \(A P\) cắt \(\left(O^{\prime}\right)\) tại \(C\) khác \(A\).
(1)) Chứng minh rằng hai tam giác \(O B P\) và \(O^{\prime} B C\) dồng dạng.
2) Gọi \(Q\) là giao điểm của hai đường thẳng \(O P\) và \(O^{\prime} C\). Chứng minh rằng \(\widehat{Q B C}+\widehat{A B P}=90^{\circ}\).
3) Lấy điểm \(D\) thuộc \((O)\) sao cho \(A D\) vuông góc \(O^{\prime} C\). Chứng minh rằng trung điểm của đoạn thẳng \(D Q\) luôn nằm trên một đường tròn cố định khi \(P\) thay đổi.
Bài 1002 (Đề thi Chuyên toán lớp 10 KHTN năm học 2023 - Vòng 2)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1355
Cho tam giác \(A B C\) nhọn với \(A B \lt A C\) nội tiếp trong đường tròn \((O)\) có tiếp tuyến tại \(A\) của \((O)\) cắt \(B C\) ở \(T\) sao cho \(T B>B C\). Gọi \(P\) và \(E\) lần lượt là trung điểm của \(T A\) và \(T C\).
1) Chứng minh rằng tứ giác \(A P E B\) nội tiếp.
2) Gọi giao điểm thứ hai của \(A E\) với \((O)\) là \(F\). Lấy \(G\) thuộc \((O)\) sao cho \(F G\) song song với \(A C\). Chứng minh rằng \(\widehat{A T G}=\widehat{T A F}\).
3) Gọi \(H\) là trực tâm của tam giác \(A B C, D\) là giao điểm của \(A H\) và \(B C . M\) là trung điểm \(B C\). K đối xứng với \(A\) qua \(B C\). \(N\) thuộc đường thẳng \(A M\) sao cho \(K N\) song song với \(H M\). Lấy \(S\) thuộc \(B C\) sao cho \(N S \perp N K\). Dựng \(R\) thuộc tia \(A K\) sao cho \(A R \cdot A H=A D^2\). \(Q\) là điểm sao cho \(P Q \perp A S\) và \(S Q \perp A O\). Chứng minh rằng điểm đối \(A R \cdot A H=A D \cdot Q\) uúng của \(A\) qua \(Q R\) thuộc đường tròn đường kính \(D N\). xứng của \(A\) qua \(Q R\) thuộc đường tròn đường kính \(D N\).
Bài 1006 (Đề thi Chuyên toán lớp 10 KHTN năm học 2022 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1358
Cho hình chữ nhật \(A B C D(A B \lt A D)\) nội tiếp trong đường tròn \((O)\). Trên cạnh \(A D\) lấy hai điểm \(E\) và \(F(E, F\) không trùng với \(A, D)\) sao cho \(E\) nằm giữa \(A\) và \(F\), đồng thời \(\widehat{A B E}+\widehat{D C F}=\dfrac{1}{2} \widehat{B O C}\).
1) Chứng minh rằng \(B E\) và \(C F\) cắt nhau tại một điểm nằm trên đường tròn \((O)\).
2) Đường thẳng qua \(O\) song song với \(B C\) cắt \(B E, C F\) theo thứ tự tại \(M, N\).
Chứng minh rằng \(\widehat{D A M}+\widehat{A D N}+\dfrac{1}{2} \widehat{A O D}=180^{\circ}\).
3) Dựng hình chữ nhật \(M N P Q\) sao cho \(N Q\) song song với \(B D\), đồng thời \(M P\) song song với \(A C\). Chứng minh rằng đường tròn ngoại tiếp hình chữ nhật \(M N P Q\) tiếp xúc với đường tròn \((O)\).
Bài 1010 (Đề thi Chuyên toán lớp 10 KHTN năm học 2022 - Vòng 2)
| 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1363
Cho tam giác \(A B C\) nhọn, không cân, nội tiếp trong đường tròn \((O)\). Điểm \(P\) nằm trong tam giác \(A B C\). Gọi \(E, F\) lần lượt là hình chiếu vuông góc của \(P\) trên các cạnh \(C A, A B\). Giả sử tứ giác \(B C E F\) nội tiếp trong đường tròn \((K)\).
1) Chứng minh rằng \(A P\) vuông góc \(B C\).
2) Chứng minh rằng \(A P=2 O K\).
3) Đường thẳng qua \(P\) vuông góc với \(A P\) cắt đường tròn \((O)\) tại hai điểm \(Q\) và \(R\). Chứng minh rằng đường tròn tâm \(A\) bán kính \(A P\) tiếp xúc với đường tròn ngoại tiếp tam giác \(K Q R\).
Bài 1015 (Đề mẫu thi Chuyên toán lớp 10 năm học 2025 - Đề số 5)
| 0 cách giải | Unknow | Độ khó: 2 | Loại: Tự luận | Lượt xem: 1000
Cho tam giác nhọn \(A B C(A B \lt A C), M\) là trung diếm của cạnh \(\mathrm{BC}, \mathrm{O}\) là tâm của đường tròn ngoại tiếp tam giác. Các đường cao \(A D, B E, C F\) của tam giác \(A B C\) đồng quy tại \(H\). Các tiếp tuyến với \((O)\) tại \(B\) và \(C\) cắt nhau tại \(S\). Gọi \(X, Y\) lần Iượt là giao điểm của đường thẳng \(E F\) với các đường thẳng \(\mathrm{BS}, \mathrm{AO}\). Chứng minh rằng:
a) \(M X \perp B F\).
b) Hai tam giác \(S M X\) và \(D H F\) đồng dạng.
c) \(\dfrac{E F}{F Y}=\dfrac{B C}{C D}\)