Bài toán chi tiết
Bài 1006 (Đề thi Chuyên toán lớp 10 KHTN năm học 2022 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1562
BẢN INCho hình chữ nhật \(A B C D(A B \lt A D)\) nội tiếp trong đường tròn \((O)\). Trên cạnh \(A D\) lấy hai điểm \(E\) và \(F(E, F\) không trùng với \(A, D)\) sao cho \(E\) nằm giữa \(A\) và \(F\), đồng thời \(\widehat{A B E}+\widehat{D C F}=\dfrac{1}{2} \widehat{B O C}\).
1) Chứng minh rằng \(B E\) và \(C F\) cắt nhau tại một điểm nằm trên đường tròn \((O)\).
2) Đường thẳng qua \(O\) song song với \(B C\) cắt \(B E, C F\) theo thứ tự tại \(M, N\).
Chứng minh rằng \(\widehat{D A M}+\widehat{A D N}+\dfrac{1}{2} \widehat{A O D}=180^{\circ}\).
3) Dựng hình chữ nhật \(M N P Q\) sao cho \(N Q\) song song với \(B D\), đồng thời \(M P\) song song với \(A C\). Chứng minh rằng đường tròn ngoại tiếp hình chữ nhật \(M N P Q\) tiếp xúc với đường tròn \((O)\).
Cách giải 1
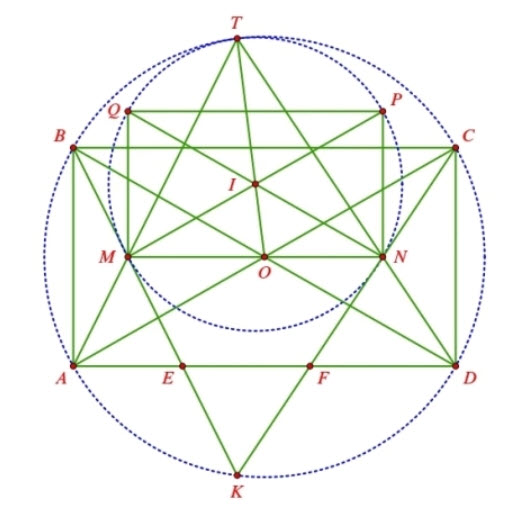
a) Do hình chữ nhật \(A B C D\) nội tiếp đường tròn \((O)\) nên \(A C, B D\) là đường kính của đường tròn \((O)\) và \(\angle A B D=\dfrac{1}{2} \angle B O C\). Suy ra \(\angle A B E+\angle D C F=\angle A B D\), từ đó
\[ \angle D B E=\angle D C F \]
Gọi \(K\) là giao điểm của hai đường thẳng \(B E\) và \(C F\). Xét tứ giác \(B K D C\), có \(\angle D B K=\angle D C K\) nên tứ giác \(B K D C\) nội tiếp, hay điểm \(K\) thuộc đường tròn \((O)\).
b) Ta có \(O M \| D E\), mà \(O\) là trung điểm của đoạn \(B D\) nên \(M\) là trung điểm của đoạn \(B E\). Ta có \(\angle B A E=90^{\circ}\), mà \(M\) là trung điểm của đoạn \(B E\) nên \(M A=M B=M E\), suy ra \(\angle E A M=\angle A E M=90^{\circ}-\angle A B E\). Tương tự, ta cũng có \(\angle F D N=90^{\circ}-\angle D C F\). Từ đó \(\angle D A M+\angle A D N=180^{\circ}-(\angle A B E+\angle D C F)=180^{\circ}-\dfrac{1}{2} \angle B O C=180^{\circ}-\dfrac{1}{2} \angle A O D\).
c) Gọi \(I\) là giao điểm của hai đường thẳng \(M P\) và \(N Q\). Ta có \(I M=I N=I P=I Q=r\) nên \((I, r)\) là đường tròn ngoại tiếp hình chữ nhật \(M N P Q\).
Do \(M P \| A C\) và \(N Q \| B D\) nên \(I M\|O A, I N\| O D\). Mà \(M N \| A D\) nên hai tam giác \(I M N\) và \(O A D\) dồng dạng \((\mathrm{g}-\mathrm{g})\), suy ra
\[ \dfrac{I M}{O A}=\dfrac{I N}{O D}=\dfrac{M N}{A D} \]
Gọi \(T\) là giao điểm của hai đường thẳng \(A M\) và \(D N\). Ta có \(M N \| C D\) nên \(\dfrac{T M}{T A}=\dfrac{M N}{A D}\), suy ra \(\dfrac{T M}{T A}=\dfrac{I M}{O A}\). Mà \(\angle T M I=\angle T A O\) nên \(\triangle T M I \sim \triangle T A O\) (c-g-c), suy ra \(\angle M T I=\angle A T O\). Từ đó, ba điểm \(T, I, O\) thẳng hàng.
Theo câu b), ta có \(\angle D A M+\angle A D N+\dfrac{1}{2} \angle A O D=\angle 180^{\circ}\). Do đó \(\angle A T D=\dfrac{1}{2} \angle A O D=\angle A B D\). Suy ra tứ giác \(A B T D\) nội tiếp, hay điểm \(T\) thuộc đường tròn \((O)\).
Do \(I M \| O A\) và \(O A=O T\) nên \(I T=I M=r\). Suy ra điểm \(T\) thuộc đường tròn \((I, r)\).
Do điểm \(T\) thuộc cả hai đường tròn \((I, r)\) và \((O)\), đồng thời ba điểm \(T, I, O\) thẳng hàng nên đường tròn \((I, r)\) tiếp xúc với đường tròn \((O)\) tại điểm \(T\).