Bài toán chi tiết

Bài 1010 (Đề thi Chuyên toán lớp 10 KHTN năm học 2022 - Vòng 2)

02-05-2025 | 2 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1090

Cách giải 1

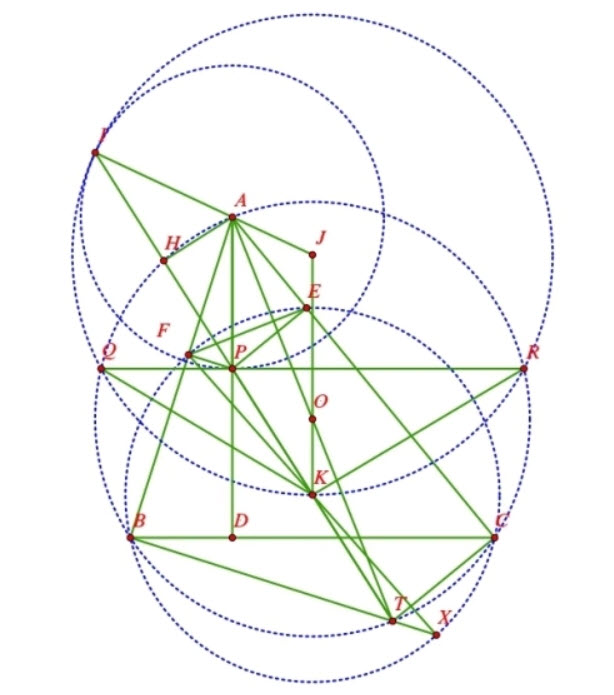
a) Gọi \(D\) là giao điểm của hai đường thẳng \(A P\) và \(B C\). Do \(\angle A E P=\angle A F P=\) \(90^{\circ}\) nên tứ giác \(A E P F\) nội tiếp, suy ra \(\angle A P E=\angle A F E\). Mà tứ giác \(B F E C\) nội tiếp nên \(\angle A C B=\angle A F E\), dẫn đến \(\angle A P E=\angle A C B\). Suy ra tứ giác \(C D P E\) nội tiếp, từ đó \(\angle A D C=\angle A E P=90^{\circ}\). Tữ đây, ta suy ra \(A P \perp B C\).

b) Gọi \(T\) và \(X\) lần lượt là các điểm đối xứng với các điểm \(P\) và \(F\) qua điểm \(K\). Ta có \(K X=K F=K B\) nên \(\angle F B X=90^{\circ}\), từ đó \(B X \| F P\). Mà \(K\) là trung điểm của các đoạn thẳng \(F X\) và \(P T\) nên \(T X \| F P\), suy ra ba điểm \(B, T, X\) thẳng hàng. Do đó \(\angle A B T=90^{\circ}\). Tương tự, ta có \(\angle A C T=90^{\circ}\). Vì vậy \(A T\) là đường kính của đường tròn \((O)\), hay \(O\) là trung điểm của đoạn \(A T\). Do \(O\) và \(K\) lần lượt là trung điểm của các đoạn thẳng \(T A\) và \(T P\) nên \(A P=2 O K\).

c) Do \(A P \perp B C, Q R \perp A P\) nên \(Q R \| B C\), mà \(O K\) là trung trực của đoạn thẳng \(B C\) nên \(O K \perp Q R\). Từ đó suy ra \(O K\) là trung trực của đoạn thẳng \(Q R\).

Gọi \(H\) là giao điểm thứ hai của đường thẳng \(T P\) và đường tròn \((O)\); \(I\) là giao điểm thứ hai của đường thẳng \(T P\) và đường tròn \((J)\) ngoại tiếp tam giác \(K Q R\).

Ta có các tứ giác \(H Q T R\) và \(K Q I R\) nội tiếp nên \(P Q \cdot P R=P H \cdot P T\) và \(P Q \cdot P R=P K \cdot P I\). Mà \(P T=2 P K\) nên ta có \(P I=2 P H\), hay \(H\) là trung điểm của đoạn thẳng \(P I\).

Lại có \(\angle A H T=90^{\circ}\) nên \(A I=A P\). Do \(A P \| K J\) nên \(\angle A P I=\angle J K I\), dẫn đến \(\angle A I P=\angle J I K\), suy ra ba điểm \(I, A, J\) thẳng hàng. Do \(I\) thuộc đường tròn \((A, A P)\) và \((J)\), đồng thời ba điểm \(I, A, J\) thẳng hàng, nên đường tròn \((A, A P)\) tiếp xúc với đường tròn \((J)\) tại \(I\). Ta có điều phải chứng minh.

Cách giải 2

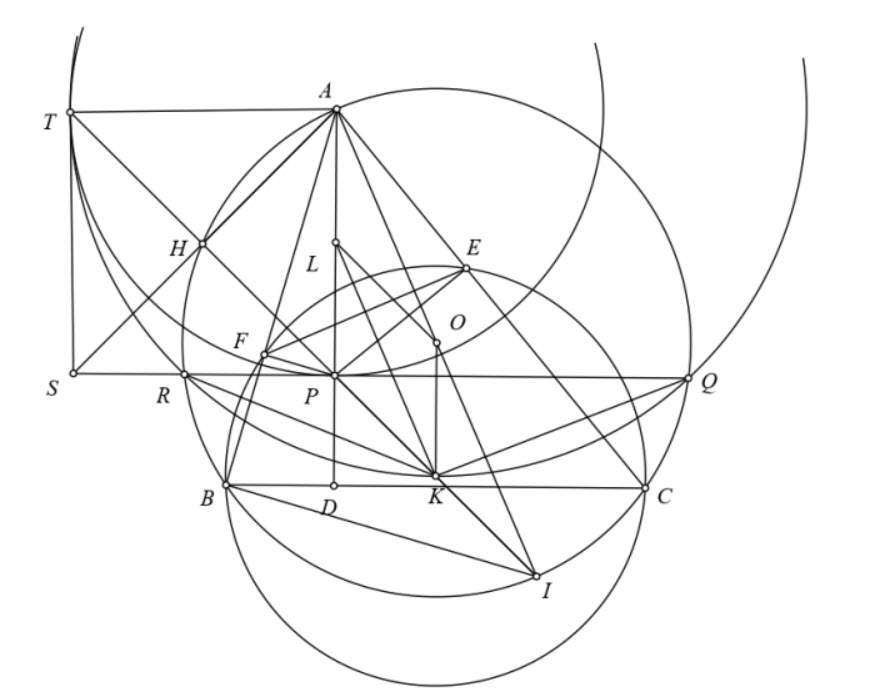
a) Gọi \(D\) là giao điểm của các đường thẳng \(A P\) và \(B C, L\) là trung điểm của đoạn thẳng \(A P\). Do \(\angle A E P=\angle A F P=90^{\circ}\) nên bốn điểm \(A, E, P, F\) cùng thuộc đường tròn \((L)\) với đường kính \(A P\).

Từ các tứ giác nội tiếp \(A E P F, B C E F\), ta có \(\angle A P E=\angle A F E=\angle B C E=\angle D C E\). Suy ra tứ giác \(C D P E\) nội tiếp. Do đó \(\angle P D C=180^{\circ}-\angle P E C=90^{\circ}\). Vì thế, \(A P \perp B C\) tại \(D\).

b) Kẻ đường kính \(A I\) của đường tròn \((O)\). Chú ý rằng tứ giác \(B C E F\) nội tiếp, ta có

\[ \angle I A E+\angle A E F=\angle I B C+\angle F B C=\angle A B I=90^{\circ} \]

Suy ra \(A I \perp E F\). Theo tính chất đường nối tâm của hai đường tròn \((K)\) và \((L)\), ta thấy \(K L \perp E F\). Do đó, \(A I \| K L\). Lại có \(A P \| O K\) (cùng vuông góc với \(B C\) ) nên \(A O K L\) là hình bình hành. Suy ra \(O K=A L=\dfrac{1}{2} A P\) hay \(A P=2 O K\).

c) Do \(A O K L\) là hình bình hành nên \(O K \| A L\) và \(O K=A L\). Vî thế, ta có \(O K \| L P\) và \(O K=L P\). Suy ra \(O K P L\) là hình bình hành. Do đó, \(O L \| P K\). Mà \(O L \| P I\) (do \(O L\) là đường trung bình của tam giác \(A P I\) ) nên ba điểm \(P, K, I\) thẳng hàng và \(P K=O L=\dfrac{1}{2} P I\). Do vậy, \(K\) là trung điểm của \(P I\).

Gọi \(H\) là giao điểm thứ hai của \(P I\) với \((O), S\) là giao điểm của \(A H\) và \(Q R, T\) là điểm đối xứng với \(P\) qua \(H\). Ta thấy \(A H \perp P T\) và \(H\) là trung điểm của \(P T\) nên \(A S\) là đường trung trực của \(P T\). Suy ra \(S P=S T, A P=A T\). Từ đó, \(T\) thuộc đường tròn \((A ; A P)\) và hai tam giác \(A P S, A T S\) bằng nhau \((\mathrm{c}-\mathrm{c}-\mathrm{c})\). Suy ra \(\angle S T A=\angle S P A=90^{\circ}\). Do đó, \(S T\) là tiếp tuyến của đường tròn \((A, A P)\).

Do tứ giác \(I Q H R\) nội tiếp và \(K, H\) lần lượt là trung điểm của \(P I, P T\), ta có

\[ P T \cdot P K=2 P H \cdot \dfrac{1}{2} P I=P H \cdot P I=P Q \cdot P R \text {. } \]

Suy ra tứ giác \(K Q T R\) nội tiếp. Áp dụng hệ thức lượng trong tam giác vuông \(A S T\) với chú ý bốn điểm \(A, H, Q, R\) cùng thuộc một đường tròn, ta có \(S T^2=S A \cdot S H=S Q \cdot S R\). Suy ra \(S T\) là tiếp tuyến của đường tròn \((T Q R)\). Hai đường tròn \((A, A P)\) và \((K Q R)\) có chung điểm \(T\) và tiếp tuyến \(S T\) nên chúng tiếp xúc nhau tại \(T\).