Bài toán chi tiết
Bài 14
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 914
BẢN IN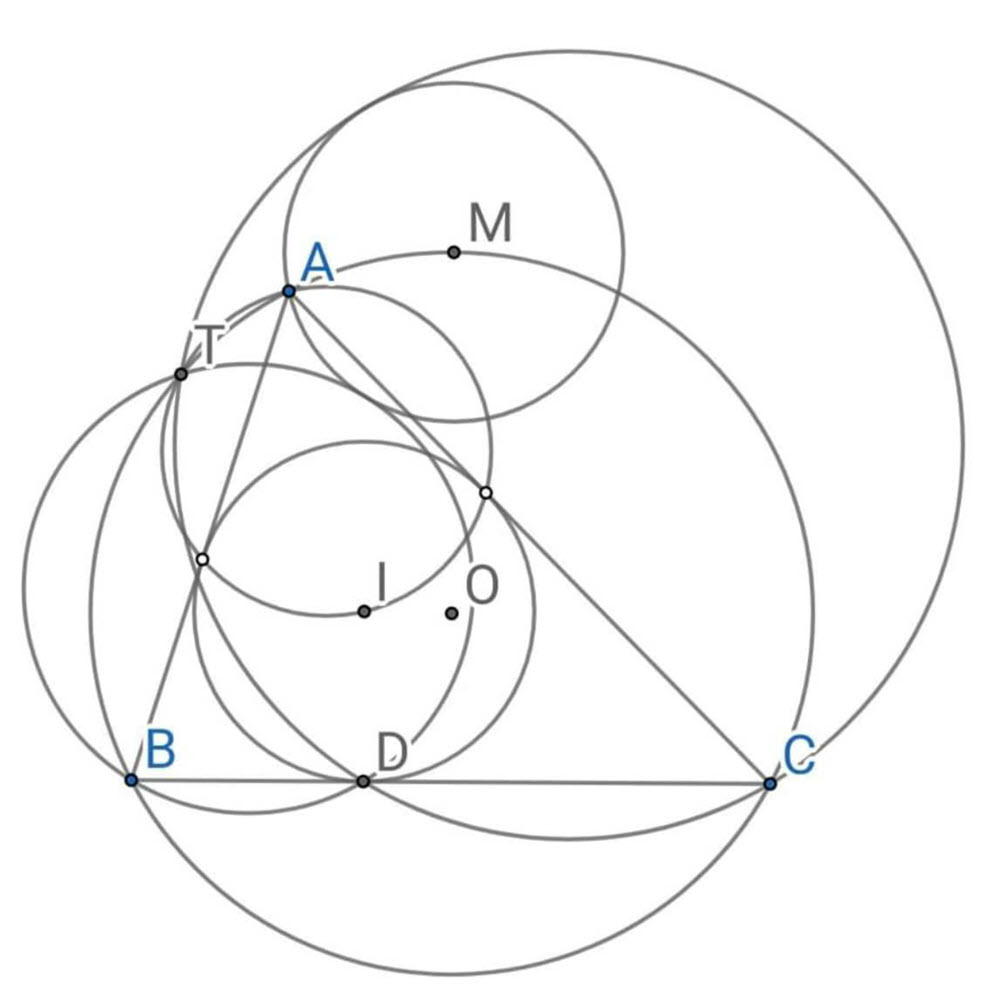
Cách giải 1
BM cắt ID tại X, TD cắt (O) tại Y, TBE đồng dạng TCF (g.g)
\[\Rightarrow \frac{TB}{TC} = \frac{EB}{FC} = \frac{BD}{DC} \Rightarrow \frac{TC}{TB} = \frac{DC}{DB} \tag{1} \]
TBD đồng dạng CYD (g.g)
\[\Rightarrow \frac{TB}{TD} = \frac{CY}{CD} \tag{2} \]
TCD đồng dạng BYD (g.g)
\[\Rightarrow \frac{TD}{TC} = \frac{BD}{BY} \tag{3} \]
Nhân (1)(2)(3) rồi rút gọn:
\[1 = \frac{CY}{DY} \Rightarrow CY=DY\]
Suy ra MY \(\perp\) BC và AIY thẳng hàng
\[\Rightarrow BTD = BTY = BMY = BXD \quad (XD//MY) \tag{*} \]
Suy ra TXDB nội tiếp, góc BXI = BMY = BAY = BAI vậy suy ra BAXI nội tiếp
\(\Rightarrow\) Góc BXA = BIA
\(\Rightarrow\) góc \(AXM = 180 - BIA = IAB + IBA = 90 - \frac{ACB}{2} \tag{4} \)
Góc \( XAM = YAM = IAX = 90 - IAX = 90 - XBI = 90 - (MBC - IBC) = 90 - (90 - BAC/2 - ABC/2)=90-ACB/2\)
Kết hợp (4) ta có góc AXM=XAM \(\Rightarrow\) MA = MB \(\tag{**}\). Từ (*) và (**) suy ra (BTD) tiếp xúc (M, MA), tương tự với (CDT) tiếp xúc (M, MA) (đpcm).