Bài toán chi tiết
Bài 937 (Thi thử Chuyên KHTN năm học 2025 - 2026 (Vòng 1))
| 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1533
BẢN INVới tứ giác \(A B C D\) lồi có hai đường chéo \(A C\) và \(B D\) cắt nhau tại \(P\). Giả sử \(Q\) là giao điểm thứ hai của các đường tròn ngoại tiếp các tam giác \(P A D\) và \(P B C\).
1) Chứng minh rằng hai tam giác \(Q D B\) và \(Q A C\) đồng dạng.
2) Chứng minh rằng \(2 \dfrac{A D}{B C} \leq \dfrac{Q D}{Q C}+\dfrac{Q A}{Q B}\).
3) Gọi \(M\) là trung diểm \(C D\). Giả sử \(Q\) nằm trong tam giác \(P C D\) và \(\angle Q P D=\angle M P C\). Chứng minh rằng \(A B C D\) là hình thang.
Cách giải 1
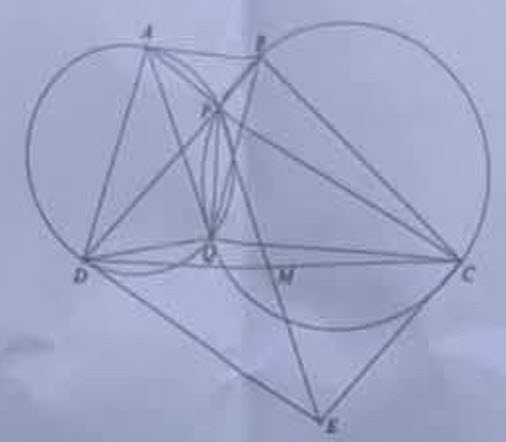
1) (1 điểm) Các tứ giác \(PQDA\) và \(PQCB\) nội tiếp nên \(\angle P D Q=\angle P A Q\) và \(\angle P B Q=\) \(\angle P C Q\). Vậy \(\triangle Q D B \sim \triangle Q A C(\mathrm{gg})\).
2) (1 điểm) Từ \(\triangle Q D B \sim \triangle Q A C\) suy ra \(\triangle Q D A \sim \triangle Q B C\) (c.g.c). Vậy
\[ 4 \frac{D A^2}{B C^2}=4 \frac{Q D}{Q B} \cdot \frac{Q A}{Q C}=4 \frac{Q D}{Q C} \cdot \frac{Q A}{Q B} \leq\left(\frac{Q D}{Q C}+\frac{Q A}{Q B}\right)^2 \]
hay
\[ 2 \dfrac{A D}{B C} \leq \dfrac{Q D}{Q C}+\dfrac{Q A}{Q B} \]
3) (1 điểm) Lấy \(E\) đối xứng \(P\) qua \(M\) thì \(P C E D\) là hình bình hành. Từ \(\angle E P C=\angle Q P D= \angle Q A D\) (giả thiết) và \(\angle P C E=\angle Q P D=\angle A Q D\) ta suy ra \(\triangle P C E \sim \triangle A Q D\) (g.g). Kết hợp 1) ta có hệ quả là
\[ \dfrac{P D}{D B}=\dfrac{E C}{D Q} \cdot \dfrac{D Q}{D B}=\dfrac{P C}{A Q} \cdot \dfrac{A Q}{A C}=\dfrac{P C}{A C} \]
Từ đẳng thức trên ta suy ra \(A B || C D\).