Bài toán chi tiết

Bài 941 (Thi thử Chuyên KHTN năm học 2025 - 2026 (Vòng 2))

01-05-2025 | 1 cách giải | Unknow | Độ khó: 4 | Loại: Tự luận | Lượt xem: 1095

Cách giải 1

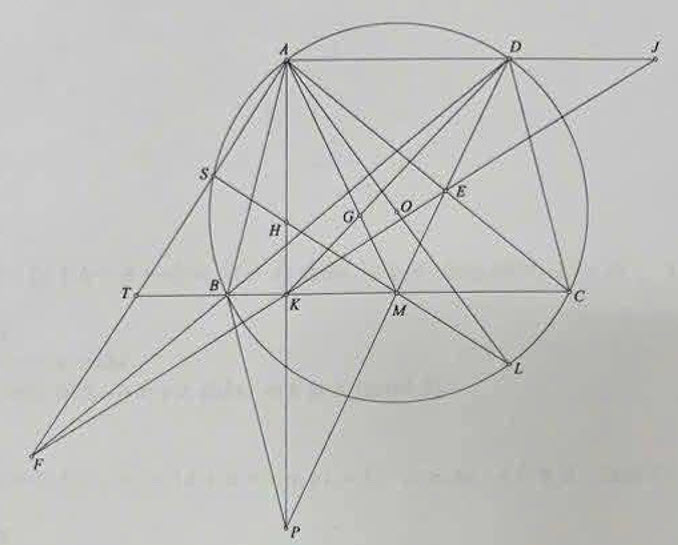
1) ( 1.5 điểm) Dễ thấy \(A B C D\) là hình thang cân. Theo tính chất đối xứng và tính chất hình thang cân thì \(\angle P B C=\angle A B C=\angle D C B\). Từ đó \(P B \| C D\). Mà \(P B=A B=C D\). Từ đó \(D B P C\) là hình bình hành, hay \(P D\) đi qua trung điểm \(M\) của \(B C\).

2) (1.0 điểm) Gọi \(G\) là trọng tâm tam giác \(A B C\) thì \(\frac{G M}{G A}=\frac{1}{2}=\frac{K M}{A D}\). Dẳng thức cuối có do tính chất đường trung bình trong tam giác \(P A D\). Từ đó hai tam giác \(G M K\) và \(G A D\) dồng dạng c.g.c nên \(K, G, D\) thẳng hàng.

3) ( 0.5 điểm) Gọi \(A L\) là đường kính của \((O)\). Dễ thấy \(B H C L\) là hình bì̀nh hành nên \(H L\) đi qua trung điểm \(M\) của \(B C\). Gọi giao điểm thứ hai của \(L H\) và \((O)\) là \(S\). Dễ thấy \(A S \perp H M\) nên \(S\) thuộc \(A F\). (Vì theo giả thiết \(A F \perp H M\) ). Gọi \(T\) là giao điểm của \(A F\) và \(B C\), dễ thấy \(H\) là trực tâm tam giác \(A T M\). Từ đó

\[ K T \cdot K M=K H \cdot K A=K B \cdot K C \]

Hệ quả là

\[ \frac{K T}{K C}=\frac{K B}{K M}=\frac{K T-K B}{K C-K M}=\frac{T B}{M C} \]

Goi \(E\) là giao điển của \(M D\) và \(A C\). Ta sẽ chứng minh \(F, K, E\) thẳng hàng. Thật vậy, gọi giao điểm của \(F K\) với \(A D\) là \(J\), ta đưa về chứng minh \(K, E, J\) thẳng hàng. Sử dụng (1), và định lý Thales ta thấy

\[ \frac{K C}{A J}=\frac{K C}{K T} \cdot \frac{K T}{A J}=\frac{M C}{T B} \cdot \frac{T B}{A D}=\frac{M C}{A D}=\frac{E C}{E A} \]

Đẳng thức (2) kết hợp với \(\angle E C K=\angle E A J\) (do \(C K \| A J\) ) thể hiện hai tam giác \(E C K\) và \(E A J\) đồng dạng (c.g.c) hay \(K, E, J\) thẳng hàng. Kết thúc chứng minh.