Bài toán chi tiết

Bài 990 (Đề thi Chuyên toán lớp 10 KHTN năm học 2024 - Vòng 1)

02-05-2025 | 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1087

Cách giải 1

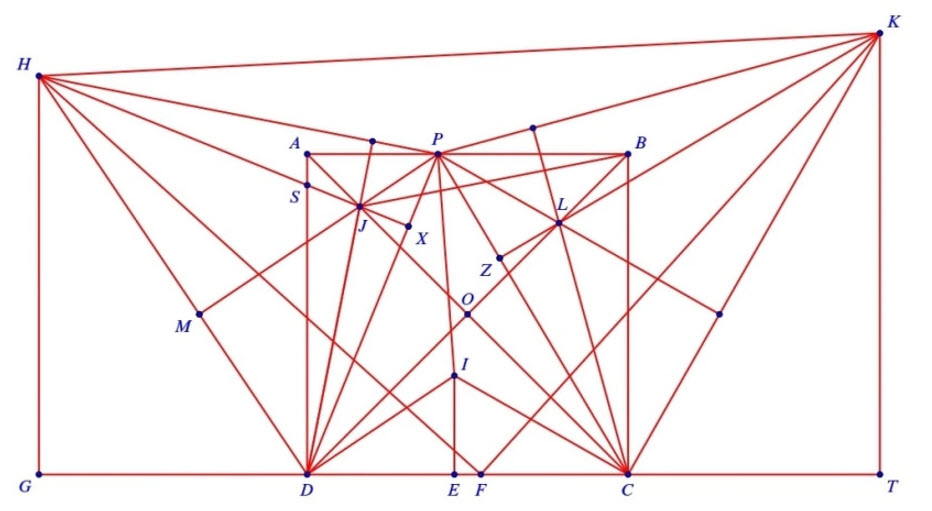
a) Hai tam giác \(A J D\) và \(A J B\) bằng nhau ( \(\mathrm{c}-\mathrm{g}-\mathrm{c}\) ) nên \(\angle A D J=\angle A B J=\angle P D J\). Từ đó suy ra tứ giác \(B D J P\) nội tiếp.

b) Gọi \(M\) là giao điểm của hai đường thẳng \(P J\) và \(H D\). Vì \(\angle D B P=45^{\circ}\) nên \(\angle M J D=45^{\circ}\), suy ra \(\angle M D J=45^{\circ}\). Từ đây, ta có \(\angle D H P=45^{\circ}\). Mặt khác, ta lại có \(\angle J H P=\angle J D P=\angle J D S\) nên \(\angle D H P-\angle S H P=\angle M D J-\angle J D S\). Từ đó \(\angle S H D=\angle S D H\), suy ra \(S H=S D\).

c) Gọi \(Z\) là giao điểm của đường thẳng \(K L\) và đường thẳng \(P C ; X\) là giao điểm của đường thẳng \(H J\) và \(P D\). Gọi \(G, T\) tương ứng là hình chiếu vuông góc của các điểm \(H, K\) trên đường thẳng \(C D\). Ta có \(\angle D H G=\angle S D H=\angle S H D\), do đó

\[ D G=D X=\dfrac{D A+D P-A P}{2} \]

Hoàn toàn tương tự, ta cũng có \(C T=C Z=\dfrac{C P+C B-B P}{2}\) và \(C F=D E=\dfrac{D C+D P-C P}{2}\). Đến đây, với chú ý tam giác \(H P D\) có \(\angle P H D=45^{\circ}\) và \(J\) là trực tâm tam giác, ta dễ dàng chứng minh được \(H J=D P\) (đây là một kết quả quen thuộc). Lại có \(J X=\dfrac{A P+A D-D P}{2}\) nên

\[ H X=\dfrac{A D+A P+D P}{2}=C F+C T=T F \]

Chứng minh tương tự, ta có \(K T=F G\). Từ đó \(\triangle G H F=\triangle T F K\) ( \(\mathrm{c}-\mathrm{g}-\mathrm{c}\) ). Từ đây, ta dễ dàng suy ra tam giác \(F H K\) vuông cân.