Bài toán chi tiết

Bài 994 (Đề thi Chuyên toán lớp 10 KHTN năm học 2024 - Vòng 2)

02-05-2025 | 1 cách giải | Unknow | Độ khó: 3 | Loại: Tự luận | Lượt xem: 1090

Cách giải 1

a) Ta có \(E F \| B C\) nên \(\angle P M F=\angle P C B=\angle P A B\), suy ra tứ giác \(A F P M\) nội tiếp. Chứng minh tương tự, ta cũng có tứ giác \(A E P N\) nội tiếp. Từ đây, ta có

\[ \angle E P F=\angle A P F+\angle A P E=\angle A M F+\angle A N E=180^{\circ}-\angle M A N=\angle Q P R \]

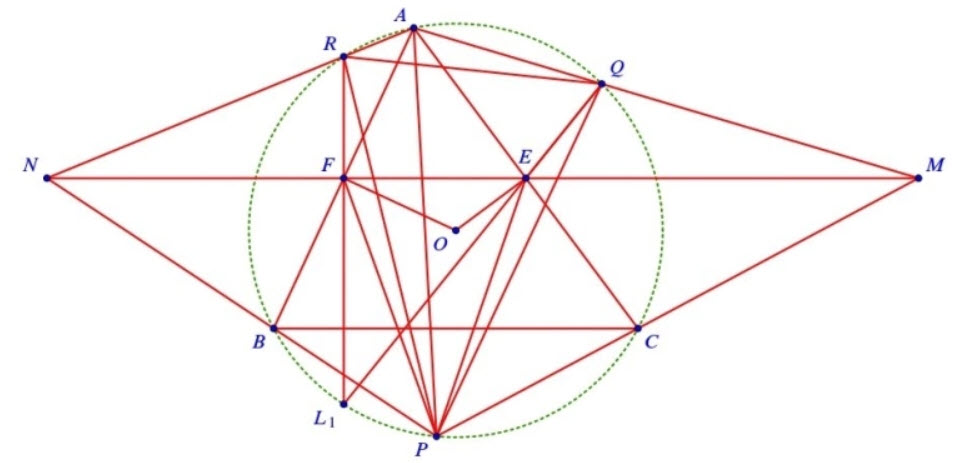
b) Ta có \(\angle P F M=\angle P A M=\angle P R Q\), mà \(\angle E P F=\angle R P Q\), nên hai tam giác \(P F E\) và \(P R Q\) đồng dạng \((\mathrm{g}-\mathrm{g})\). Từ đây, ta dễ dàng suy ra hai tam giác \(P F R\) và \(P E Q\) đồng dạng (c-g-c). Từ đó \(\angle P R F=\angle P Q E\).

Bây giờ, gọi \(L_1\) là giao điểm của hai đường thẳng \(Q E\) và \(R F\). Thế thì tứ giác \(P L_1 R Q\) là tứ giác nội tiếp, từ đó suy ra điểm \(L_1\) thuộc đường tròn \((O)\).

c) Ta có bổ đề sau.

Bổ đề. Cho tứ giác \(A B C D\) nội tiếp đường tròn \((O)\), các đường chéo \(A C\) và \(B D\) cắt nhau tại điểm I. Gọi \(H\) là hình chiếu vuông góc của điểm I trên đuoờng thẳng \(C D\) và \(M\) là trung điểm của đoạn thẳng \(C D\). Các điểm \(N, P\) lần lượt thuộc các đuờng thẳng \(B C, A D\) sao cho \(M N \| A C\) và \(M P \| B D\). Đường tròn ngoại tiếp tam giác \(M N P\) cắt đường thẳng \(C D\) lần thứ hai tại điểm \(K\). Khi đó, \(M\) là trung điểm của đoạn thẳng \(H K\).

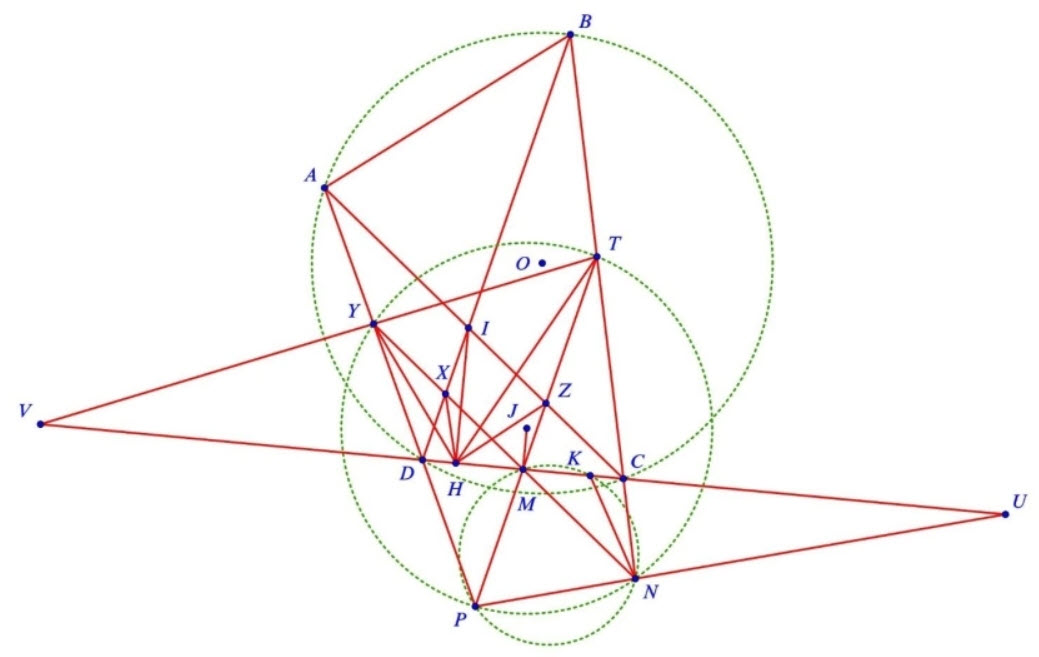
Chứng minh. Gọi \(X, Y\) lần lượt là giao điểm của đường thẳng \(M N\) và các đường thẳng \(D I\), \(D A ; Z, T\) lần lượt là giao điểm của đường thẳng \(M P\) và các đường thẳng \(C I, C B\). Ta thấy \(X\), \(Y, Z, T\) lần lượt là trung điểm của các đoạn thẳng \(D I, D A, C I, C B\) và tứ giác \(M H X Z\) là hình thang cân.

Từ \(\angle H X Y=\angle H Z T\) và \(\dfrac{X H}{X Y}=\dfrac{I D}{I A}=\dfrac{I C}{I B}=\dfrac{Z H}{Z T}\), ta suy ra \(\triangle H X Y \sim \triangle H Z T\) (c-g-c). Từ đó \(\angle H Y X=\angle H T Z\). Suy ra, tứ giác \(H M T Y\) nội tiếp.

Chú ý rằng \(N Y \| A C\) và \(P T \| B D\), ta có \(\angle N Y P=\angle D A C=\angle D B C=\angle N T P\). Suy ra, tứ giác \(N P Y T\) nội tiếp.

Gọi \((J)\) là đường tròn ngoại tiếp tứ giác \(N P Y T\). Do \(M\) là trung điểm của đoạn thẳng \(C D\) nên theo định lý con bướm đảo, ta có \(J M \perp C D\). Gọi \(U, V\) lần lượt là giao điểm của đường thẳng \(C D\) và các đường thẳng \(N P Y T\). Áp dụng định lý con bướm thuận, ta có \(M\) là trung điểm của đoạn thẳng \(U V\).

Vì \(\angle N Y T=\angle N P T=\angle U K N\) nên tứ giác \(N K Y V\) nội tiếp. Chứng minh tương tự, tứ giác \(N H Y U\) nội tiếp. Suy ra \(M H \cdot M U=M N \cdot M Y=M K \cdot M V\). Lại có \(M U=M V\) nên \(M H=M K\). Vậy, \(M\) là trung điểm của đoạn thẳng \(H K\). Bổ đề được chứng minh.

Trở lại bài toán, ta xét trường hợp các điểm ở vị trí như trong hình vẽ (xem trang sau), các trường hợp còn lại chứng minh tương tự.

Gọi \(X\) là giao điểm khác \(F\) của đường tròn \((K)\) và đường thẳng \(A B\). Qua điểm \(D\), kẻ đường thẳng vuông góc với đường thẳng \(A B\) tại điểm \(Y\). Gọi \(Z, G\) lần lượt là giao điểm của đường thẳng \(K J\) và các đường thẳng \(A B, E F\). Gọi \(H\) là giao điểm của hai đường thẳng \(L J\) và \(E F\) tại \(H\). Gọi \(U, V\) lần lượt là giao điểm của đường thẳng \(B C\) và các đường thẳng \(O E, O F\).

Áp dụng bổ đề trên, ta có \(F\) là trung điểm của đoạn thẳng \(X Y\).

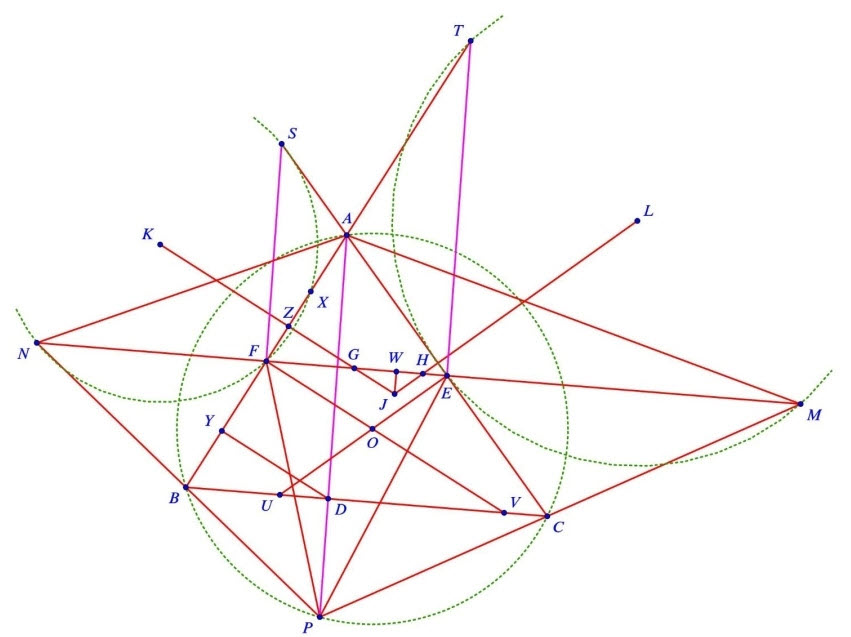
Do \(\dfrac{F G}{F Z}=\dfrac{B D}{B Y}=\dfrac{D V}{F Y}\) và \(F Y=F X=2 F Z\) nên \(F G=\dfrac{D V}{2}\). Lập luận tương tự, ta cũng có \(E H=\dfrac{D U}{2}\). Do đó \(F G+H E=\dfrac{U V}{2}\). Suy ra \(G H=E F-(F G+E H)=\dfrac{B C-U V}{2}\) không đổi. Tam giác \(J G H\) có các góc khồng đổi và cạnh \(G H\) có độ dài không đổi nên đường cao \(J W\) của tam giác có độ dài bằng \(h\) không đổi. Vậy, điểm \(J\) thuộc đường thẳng song song \(E F\) cách \(E F\) một khoảng bằng \(h\) cố định.