Bài toán chi tiết
Bài 998 (Đề thi Chuyên toán lớp 10 KHTN năm học 2023 - Vòng 1)
| 1 cách giải | Unknow | Độ khó: 1 | Loại: Tự luận | Lượt xem: 1299
BẢN INCho hai đường tròn \((O)\) và \(\left(O^{\prime}\right)\) cố định cắt nhau tại \(A\) và \(B\) sao cho \(O\) nằm ngoài \(\left(O^{\prime}\right)\) và \(O^{\prime}\) nằm ngoài \((O)\). Trên đường tròn \((O)\) lấy điểm \(P\) di chuyển sao cho \(P\) nằm trong đường tròn \(\left(O^{\prime}\right)\). Đường thẳng \(A P\) cắt \(\left(O^{\prime}\right)\) tại \(C\) khác \(A\).
(1)) Chứng minh rằng hai tam giác \(O B P\) và \(O^{\prime} B C\) dồng dạng.
2) Gọi \(Q\) là giao điểm của hai đường thẳng \(O P\) và \(O^{\prime} C\). Chứng minh rằng \(\widehat{Q B C}+\widehat{A B P}=90^{\circ}\).
3) Lấy điểm \(D\) thuộc \((O)\) sao cho \(A D\) vuông góc \(O^{\prime} C\). Chứng minh rằng trung điểm của đoạn thẳng \(D Q\) luôn nằm trên một đường tròn cố định khi \(P\) thay đổi.
Cách giải 1
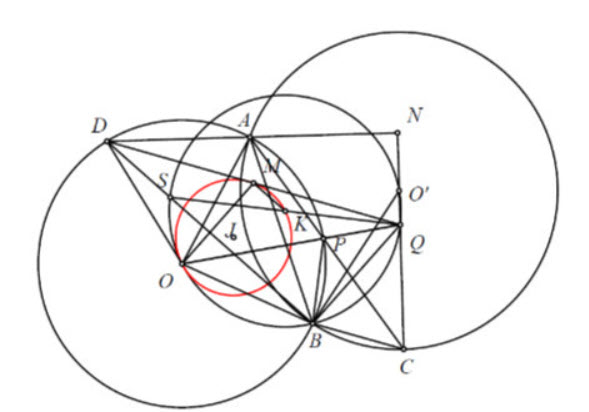
1. Ta có \(\angle P O B=2 \angle P A B=\angle B O^{\prime} C\) nên hai tam giác \(O B P\) và \(O^{\prime} B C\) dồng dạng.
2. Từ câu 1) ta thu được \(\angle O P B=\angle O^{\prime} C B\) nên tứ giác \(B P Q C\) nội tiếp. Suy ra \(\angle Q B C=\) \(\angle Q P C=\angle A P O=90^{\circ}-\dfrac{1}{2} \angle A O P=90^{\circ}-\angle A B P\).
3. \(C Q\) cắt \(A D\) tại \(N . M\) là trung điểm của \(D Q\).
Ta có \(\angle B Q C=\angle B P C=\angle B A N\) nên tứ giác \(D N Q B\) nội tiếp.
Suy ra \(\angle D B Q=90^{\circ}\).
Suy ra \(M D=M B=M Q\), ta thu được \(O M \perp B D\).
Từ câu 1) ta cũng có \(\angle B O Q=\angle B O^{\prime} Q\) nên tứ giác \(B O O^{\prime} Q\) nội tiếp \((K)\).
Kẻ đường kính \(Q S\) của \((K)\) thì \(D, S, B\) thẳng hàng.
Ta có \(M K \| D S\) nên \(\angle O M K=90^{\circ}\). Do \(O, B, O^{\prime}\) cố định nên \(K\) cố định.
Vậy \(M\) chuyển động trên đường tròn đường kính \(O K\) cố định.