Bài 1
(2 điểm)
1. Giải phương trình:
\[ \sqrt{4-3 x}+\sqrt{3 x-2}=\dfrac{3 x^2-2 x+3}{x^2+1} \]
2. Với \(x, y\) là các số tự nhiên thỏa mãn: \(x+y+1\) là số nguyên tố và \(x+y+1\) là một ước của \(2\left(x^2+y^2\right)-1\). Chứng minh: \(x=y\).
Bài 2
(2 điểm)
1. Tìm tất cả các bộ 4 số nguyên dương \((a ; b ; c ; p)\) trong đó \(p, p+2\) là số nguyên tố lẻ, sao cho \(2^a \cdot p^b=(p+2)^c-1\).
2. Tìm tất cả các giá trị nguyên của \(m\) để tất cả các nghiệm của đa thức \(P(x)=3 x^3-3 x^2+m\) đều là các số hữu tỉ.
Bài 3
(2 điểm)
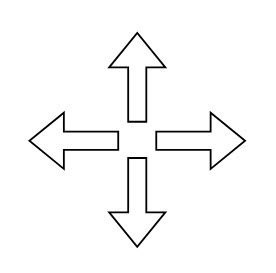
1. Bạn An chơi game trên máy tính điện tử, máy có phím di chuyển như hình bên. Mỗi lần nhấn phím di chuyển, nhân vật trong game sẽ di chuyển theo hướng mũi tên và độ dài mỗi bước đi là như nhau. Tính xác suất để sau bốn lần di chuyển, nhân vật trong game trở về đúng vị trí ban đầu.
2. Với các số thực \(a, b, c\) thỏa mãn: \(0 \leq a, b, c \leq 1\). Tìm giá trị lớn nhất của biểu thức:
\[ P=\dfrac{a}{\sqrt{2 b c+1}}+\dfrac{b}{\sqrt{2 c a+1}}+\dfrac{c}{\sqrt{2 a b+1}} \]
Bài 4
(3 điểm)
Cho tứ giác \(A B C D\) nội tiếp đường tròn \((O)\) với 2 đường chéo \(A C, B D\) vuông góc với nhau và không đi qua tâm. Trên đường tròn ngoại tiếp tam giác \(B O D\) lấy các điểm \(X, Y\) sao cho \(\widehat{A X O}=\widehat{C Y O}=90^{\circ}\). Gọi \(M\) là trung điềm của \(A C, T\) là giao điểm của \(A C, B D\), tia \(O T\) cắt đường tròn \(c_1\) ngoại tiếp tam giác \(B O D\) tại \(S\).
1. Chứng minh: \(O D^2=O T . O S\) và \(\widehat{X A T}=\widehat{X S T}\).
2. Chứng minh: \(B D\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(M X Y\).
Bài 5
(1 điểm)
Quân vua được đặt trên bàn cờ là bảng ô vuông \(8 \times 8\). Giả sử ta có 64 lần di chuyển quân vua đi qua tất cả các ô trên bàn cờ để quay về vị trí ban đầu. Tại mỗi thời điểm, khoảng cách từ tâm ô mà quân vua đang đứng đến tâm của toàn bộ bàn cờ đều được tính toán. Một nước đi được gọi là ''dễ chịu" nếu sau mỗi nước đi khoảng cách này nhỏ hơn so với khoảng cách trước khi di chuyển. Tìm số lượng nước đi "dễ chịu" lớn nhất có thể?