Bài 1
(2 điểm)
a) Xét đa thức \(f(x)=2 x^3-3 x^2+4 x-5\). Tính tổng
\[ S=f\left(\dfrac{1}{2025}\right)+f\left(\dfrac{2}{2025}\right)+\cdots+f\left(\dfrac{2024}{2025}\right)\]
b) Cho hai số thực \(a, b\) thoả mãn điều kiện sau \( \dfrac{1}{a}+\dfrac{1}{b}=1\) và \(\dfrac{1}{a+1}+\dfrac{1}{b+1}-\dfrac{1}{a+b}=\dfrac{1}{2}\)
Tính
\[ P = a^4 + b^4 \]
Bài 2
(2 điểm)
a) Cho \(a, b, c\) là ba số thực phân biệt thỏa mãn \(\dfrac{a^3+1}{a}=\dfrac{b^3+1}{b}=\dfrac{c^3+1}{c}\). Chứng minh rà̀ng \(a b c+1=0\).
b) Chứng minh \(a=\sqrt[3]{3 + \sqrt{8}}+\sqrt[3]{3-\sqrt{8}}\) là số vô tỷ.
Bài 3
(2 điểm)
1) Cho \(x_1 ; x_2 ; \ldots ; x_{10}\) là các số nguyên dương thỏa mãn \(x_1+x_2+\ldots+x_{10}=100\). Tìm giá trị lớn nhất của biểu thức \(P=x_1 \cdot x_2+x_2 \cdot x_3+\ldots+x_9 \cdot x_{10}\).
2)
a) Tìm tất các số nguyên tố \(p, q, r\) thỏa mãn \(\dfrac{1}{p}+\dfrac{1}{q}+\dfrac{1}{r}+\dfrac{1}{p q r}=1\)
b) Tìm số tự nhiên \(n\) sao cho \(2^{2025}+2^{2022}+2^n\) là số chính phương.
Bài 4
(2 điểm)
Một Latin Square cấp \(n\) là một-bảng số \(n \times n\) gồm \(n\) hàng và \(n\) cột, trong đó mỗi ô của bảng chỉ nhận một số từ tập \(A=\{1 ; 2 ; \ldots ; n\}\) (gồm \(n\) số) sao cho trên mỗi hàng, mỗi cột mỗi số xuất hiện đúng một lần. Ví dụ sau là một Latin Square cấp 3 .
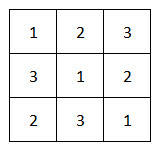
Hai ô được gọi là cạnh nhau nếu chúng có chung eạnh. Một bước dịch chuyển là từ vị trí ô này nhảy sang vị trí ô bên cạnh. Một đường đi Ất Ty là một loạt các bước dịch chuyển liên tục đi qua tất cả các ô, mỗi ô đúng một lần và đi theo thứ tự lặp lại \(1,2, \ldots, n, 1,2 \ldots, n, \ldots\).
a) Chỉ ra có một Latin Square cấp 4 chứa một đường đi Ất Ty.
b) Chứng minh rằng không bao giờ có một đường đi Ất Ty trong một Latin Square cấp 5 .
Bài 5
(2 điểm)
Tam giác nhọn \(A B C\) nội tiếp đường tròn \((O)\) có 3 đường cao \(A D, B E, C F\) cắt nhau tại \(H\). Dựng đường thẳng qua \(H\) cắt \(A B, A C\) lần lượt tại \(P, Q\) sao cho \(\triangle A P Q\) cân tại \(A\). Dựng đường kính \(A K\) của \((O)\). Đường phân giác trong của \(\widehat{B A C}\) cắt \(H K\) tại \(S\).
a) Chứng minh: \(B H C K\) là hình bình hành và hai tam giác \(\triangle A F H, \triangle A C K\) dồng dạng.
b) Chứng minh: \(H P\) là phân giác của \(\widehat{F H B}\).
c) Chứng minh: \(S\) nằm trên đường tròn ngoại tiếp tam giác \(A P Q\)