Bài 1
(3 điểm)
1) Giải phương trình
\[ \sqrt{x+1}+\sqrt{1-x}+\sqrt{1-x^2}=3 \]
2) Giải hệ phương trình
\[ \left\{\begin{array}{l} 3 x^2+2 y^2+7 x y=12 \\ x^3+3 x^2 y+2 y^2 x+2 x+4 y=12 \end{array}\right. \]
Bài 2
(3 điểm)
1) Tìm \(x, y\) nguyên thỏa mān
\[ y=\dfrac{x+1}{x^4+1} \]
2) Với \(a, b, c\) là những số thực dương thỏa mãn \(a b+b c+c a=1\). Tìm giá trị nhỏ nhất của biểu thức
\[ P=2 a^2+b^2+c^2 \]
Bài 3
(3 điểm)
Cho hình thang \(A B C D\) nội tiếp đường tròn \((O)\) với \(A D || B C\) và \(A D \lt B C\). Giả sử tam giác \(A B C\) nhọn, không cân. Gọi \(P\) là điểm đối xứng của \(A\) qua \(B C\).
1) Chứng minh rằng \(D P\) đi qua trung điểm \(M\) của \(B C\).
2) Gọi \(K\) là trung điểm \(A P\). Chứng minh rằng \(K D\) đi qua trọng tâm tam giác \(A B C\).
3) Goi \(H\) là trực tâm tam giác \(A B C\). Giả sử có \(F\) nằm trên đường thẳng \(B D\) sao cho \(A F \perp H M\). Chứng minh rằng \(F K, A C, P D\) đồng quy.
Bài 4
(1 điểm)
Với \(n\) nguyên, \(n \geq 3\), hãy tìm \(n\) để có thể viết các số \(1,2,3, \ldots, n^2\) vào các ô vuông của bảng \((n \times n)\) mỗi ô đúng một số, sao cho tổng 4 số trên các hình bất kỳ dạng
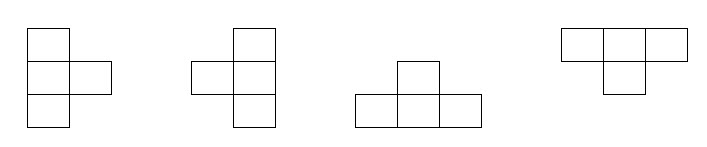
của bảng đều là số chẵn.