Bài 1
(2 điểm)
1) Giải hệ phương trình
\[ \left\{\begin{array}{l} 6(x y+5)+x^3 y+5 x^2=42 \\ x^3+5 x^2 y+6 x+30 y=42 \end{array}\right. \]
2) Giải phương trình
\[ (\sqrt[3]{x+6}+\sqrt[3]{3-x})(2+3 \sqrt[3]{(x+6)(3-x)})=24 \]
Cách giải 1:
a) Hệ phương trình đã cho có thể được viết lại thành
\[ \left\{\begin{array}{l} \left(x^2+6\right)(x y+5)=42 \\ \left(x^2+6\right)(x+5 y)=42 \end{array}\right. \]
Từ đây, ta suy ra \(x y+5=x+5 y\), hay \((x-5)(y-1)=0\). Từ đó \(x=5\) hoặc \(y=1\).
- Với \(x=5\), phương trình thứ hai của hệ có thể được viết lại thành \(31(5+5 y)=42\). Giải phương trình này, ta được \(y=-\dfrac{113}{155}\). Thử lại, ta thấy thỏa mãn.
- Với \(y=1\), phương trình thứ nhất của hệ có thể được viết lại thành \(\left(x^2+6\right)(x+5)=42\). Giải phương trình này, ta được \(x=1\). Thử lại, ta thấy thỏa mãn.
Vậy hệ phương trình đã cho có hai nghiệm \((x, y)\) là \((1,1)\) và \(\left(5,-\dfrac{113}{155}\right)\).
b) Đặt \(a=\sqrt[3]{x+6}\) và \(b=\sqrt[3]{3-x}\). Khi đó, ta có \(a^3+b^3=9\). Ngoài ra, từ phương trình đã cho, ta cũng có \((a+b)(2+3 a b)=24\). Do đó
\[ 33=a^3+b^3+(a+b)(2+3 a b)=(a+b)^3+2(a+b) \]
Từ đây, ta dễ dàng suy ra \(a+b=3\). Từ đó \(a b=2\). Và như thế, dễ thấy \(a=2, b=1\) hoặc \(a=1, b=2\). Bằng cách xét từng trường hợp cụ thể, ta thấy phương trình đã cho có hai nghiệm là \(x=2\) và \(x=-5\).
Bài 2
(2 điểm)
1) Tìm tất cả các cặp số nguyên \((x, y)\) thỏa mãn đẳng thức
\[ 25 y^2+354 x+60=36 x^2+305 y+(5 y-6 x)^{2022} \]
2) Trên bàn có 8 hộp rỗng (trong các hộp không có viên bi nào). Người ta thực hiện các lần thêm bi vào các hộp theo qui tắc sau: mỗi lần ta chọn ra 4 hộp bất kỳ và bỏ vào một hộp 1 viên, một hộp 2 viên, hai hộp còn lại mỗi hộp 3 viên. Hỏi số lần thêm bi ít nhất có thể để nhận được số bi ở 8 hộp trên là 8 số tự nhiên liên tiếp?
Cách giải 1:
a) Đặt \(a=6 x\) và \(b=5 y\), phương trình đã cho có thể được viết lại thành
\[ b^2+59 a+60=a^2+61 b+(b-a)^{2022} \]
hay
\[ (b-a-1)(a+b-60)=(b-a)^{2022} \]
Từ đây, dễ thấy \(b-a-1 \neq 0\). Cũng từ \((1)\), ta suy ra \((b-a)^{2022}\) chia hết cho \(b-a-1\). Mà \((b-a, b-a-1)=1\) nên \(b-a-1 \in\{1,-1\}\), hay \(b-a \in\{2,0\}\).
- Với \(b-a=0\), từ phương trình (1), ta có \(a+b=60\). Suy ra \(a=b=30\), tức \(x=5\) và \(y=6\). Thử lại, ta thấy thỏa mãn.
- Với \(b-a=2\), từ phương trình (1), ta có \(a+b-60=2^{2022}\). Do đó \(b=2^{2021}+31\). Tuy nhiên, ta lại có \(2^{2021}+31 \equiv 3(\bmod 5)\) nên \(b \equiv 3(\bmod 5)\), mâu thuẫn.
Vậy chỉ có duy nhất một cặp số nguyên \((x, y)\) thỏa mãn yêu cầu là \((5,6)\).
b) Có thể thấy rằng, sau mỗi lần thêm bi, số viên bi tăng thêm 9 viên bi. Do đó, tổng số viên bi ở tất cả các hộp không thay đổi số dư khi chia cho 9 . Suy ra tổng số viên bi ở tất cả các hộp luôn chia hết cho 9 .
Nếu số viên bi ở các hộp là \(0,1, \ldots, 7\) thì tổng số viên bi ở tất cả các hộp là \(0+1+\cdots+7=28\), chia 9 dư 1 , mâu thuẫn. Do đó, tổng số viên bi ở các hộp không nhỏ hơn \(1+2+\cdots+8=36\). Từ đây, suy ra số lần thêm bi không ít hơn \(\dfrac{36}{9}=4\).
Mặt khác, ta thấy cách thêm bi như sau thỏa mãn sau bốn lần số viên bi ở các hộp lần lượt là 1 , \(2, \ldots, 8\) (các hộp giữ nguyên thứ tự trong suốt quá trình thêm bi):
- Lần 0: \(0,0,0,0,0,0,0,0\).
- Lần 1: \(1,2,3,3,0,0,0,0\).
- Lần 2: 1, 2, 3, 6, 3, 2, 1, 0 .
- Lần 3: \(1,2,3,6,6,5,3,1\).
- Lần 4: 1, 2, 3, 6, 7, 8, 5, 4 .
Vậy số lần thêm bi ít nhất là 4 lần.
Bài 3
(3 điểm)
Cho hình chữ nhật \(A B C D(A B \lt A D)\) nội tiếp trong đường tròn \((O)\). Trên cạnh \(A D\) lấy hai điểm \(E\) và \(F(E, F\) không trùng với \(A, D)\) sao cho \(E\) nằm giữa \(A\) và \(F\), đồng thời \(\widehat{A B E}+\widehat{D C F}=\dfrac{1}{2} \widehat{B O C}\).
1) Chứng minh rằng \(B E\) và \(C F\) cắt nhau tại một điểm nằm trên đường tròn \((O)\).
2) Đường thẳng qua \(O\) song song với \(B C\) cắt \(B E, C F\) theo thứ tự tại \(M, N\).
Chứng minh rằng \(\widehat{D A M}+\widehat{A D N}+\dfrac{1}{2} \widehat{A O D}=180^{\circ}\).
3) Dựng hình chữ nhật \(M N P Q\) sao cho \(N Q\) song song với \(B D\), đồng thời \(M P\) song song với \(A C\). Chứng minh rằng đường tròn ngoại tiếp hình chữ nhật \(M N P Q\) tiếp xúc với đường tròn \((O)\).
Cách giải 1:
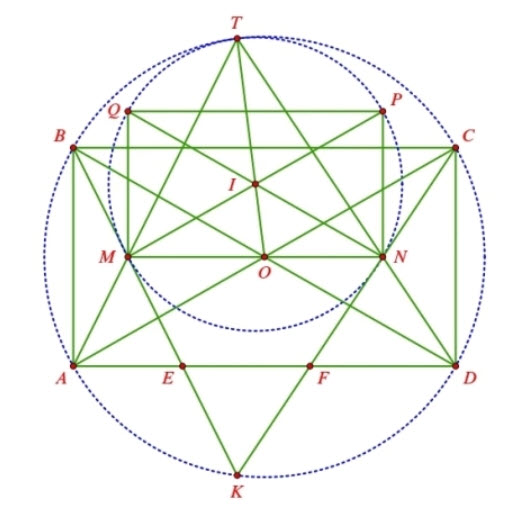
a) Do hình chữ nhật \(A B C D\) nội tiếp đường tròn \((O)\) nên \(A C, B D\) là đường kính của đường tròn \((O)\) và \(\angle A B D=\dfrac{1}{2} \angle B O C\). Suy ra \(\angle A B E+\angle D C F=\angle A B D\), từ đó
\[ \angle D B E=\angle D C F \]
Gọi \(K\) là giao điểm của hai đường thẳng \(B E\) và \(C F\). Xét tứ giác \(B K D C\), có \(\angle D B K=\angle D C K\) nên tứ giác \(B K D C\) nội tiếp, hay điểm \(K\) thuộc đường tròn \((O)\).
b) Ta có \(O M \| D E\), mà \(O\) là trung điểm của đoạn \(B D\) nên \(M\) là trung điểm của đoạn \(B E\). Ta có \(\angle B A E=90^{\circ}\), mà \(M\) là trung điểm của đoạn \(B E\) nên \(M A=M B=M E\), suy ra \(\angle E A M=\angle A E M=90^{\circ}-\angle A B E\). Tương tự, ta cũng có \(\angle F D N=90^{\circ}-\angle D C F\). Từ đó \(\angle D A M+\angle A D N=180^{\circ}-(\angle A B E+\angle D C F)=180^{\circ}-\dfrac{1}{2} \angle B O C=180^{\circ}-\dfrac{1}{2} \angle A O D\).
c) Gọi \(I\) là giao điểm của hai đường thẳng \(M P\) và \(N Q\). Ta có \(I M=I N=I P=I Q=r\) nên \((I, r)\) là đường tròn ngoại tiếp hình chữ nhật \(M N P Q\).
Do \(M P \| A C\) và \(N Q \| B D\) nên \(I M\|O A, I N\| O D\). Mà \(M N \| A D\) nên hai tam giác \(I M N\) và \(O A D\) dồng dạng \((\mathrm{g}-\mathrm{g})\), suy ra
\[ \dfrac{I M}{O A}=\dfrac{I N}{O D}=\dfrac{M N}{A D} \]
Gọi \(T\) là giao điểm của hai đường thẳng \(A M\) và \(D N\). Ta có \(M N \| C D\) nên \(\dfrac{T M}{T A}=\dfrac{M N}{A D}\), suy ra \(\dfrac{T M}{T A}=\dfrac{I M}{O A}\). Mà \(\angle T M I=\angle T A O\) nên \(\triangle T M I \sim \triangle T A O\) (c-g-c), suy ra \(\angle M T I=\angle A T O\). Từ đó, ba điểm \(T, I, O\) thẳng hàng.
Theo câu b), ta có \(\angle D A M+\angle A D N+\dfrac{1}{2} \angle A O D=\angle 180^{\circ}\). Do đó \(\angle A T D=\dfrac{1}{2} \angle A O D=\angle A B D\). Suy ra tứ giác \(A B T D\) nội tiếp, hay điểm \(T\) thuộc đường tròn \((O)\).
Do \(I M \| O A\) và \(O A=O T\) nên \(I T=I M=r\). Suy ra điểm \(T\) thuộc đường tròn \((I, r)\).
Do điểm \(T\) thuộc cả hai đường tròn \((I, r)\) và \((O)\), đồng thời ba điểm \(T, I, O\) thẳng hàng nên đường tròn \((I, r)\) tiếp xúc với đường tròn \((O)\) tại điểm \(T\).
Bài 4
(1 điểm)
Cho \(a, b, c\) là những số thực dương. Chứng minh rằng
\[ \dfrac{2 a}{a+b}+\dfrac{a+b}{a+c}+\dfrac{6 a+2 c}{3 b+c}+\dfrac{4 a+3 b+c}{b+c} \geq \dfrac{32 a}{2 a+b+c} \]
Cách giải 1:
Sử dụng các bất đẳng thức AM-GM và Cauchy-Schwarz , ta có
\[ \begin{aligned} \mathrm{VT}_{(1)} & =\left(\dfrac{2 a}{a+b}+\dfrac{a+b}{a+c}\right)+\left[\dfrac{2(3 a+c)}{3 b+c}+\dfrac{3 b+c}{b+c}\right]+\dfrac{4 a}{b+c} \\ & \geq 2 \sqrt{\dfrac{2 a}{a+c}}+2 \sqrt{\dfrac{2(3 a+c)}{b+c}}+\dfrac{4 a}{b+c}=\dfrac{4 a}{\sqrt{2 a(a+c)}}+2 \sqrt{\dfrac{2(3 a+c)}{b+c}}+\dfrac{4 a}{b+c} \\ & \geq \dfrac{8 a}{3 a+c}+2 \sqrt{\dfrac{2(3 a+c)}{b+c}}+\dfrac{4 a}{b+c}=\left[\dfrac{8 a}{3 a+c}+\sqrt{\dfrac{2(3 a+c)}{b+c}}+\sqrt{\dfrac{2(3 a+c)}{b+c}}\right]+\dfrac{4 a}{b+c} \\ & \geq 3 \sqrt[3]{\dfrac{16 a}{b+c}}+\dfrac{4 a}{b+c}=\dfrac{12 a}{\sqrt[3]{2 a \cdot 2 a \cdot(b+c)}}+\dfrac{4 a}{b+c} \geq \dfrac{36 a}{4 a+b+c}+\dfrac{4 a}{b+c} \\ & =4 a\left(\dfrac{9}{4 a+b+c}+\dfrac{1}{b+c}\right) \geq 4 a \cdot \dfrac{(3+1)^2}{4 a+b+c+b+c}=\dfrac{32 a}{2 a+b+c} \end{aligned} \]
Dấu đẳng thức xảy ra khi và chỉ khi \(a=b=c\)