Bài 1
(2 điểm)
1) Với \(a, b, c\) là những số thực dương thỏa mãn điều kiện \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1\). Chứng minh rằng
\[ \dfrac{1}{2}\left(\dfrac{1}{a+b c}+\dfrac{1}{b+c a}+\dfrac{1}{c+a b}\right)=\sqrt{\dfrac{a b c}{(a+b c)(b+c a)(c+a b)}} \]
2) Giải hệ phương trình
\[ \left\{\begin{array}{l} 2 x^2+3 x y+y^2=6 \\ 3 x+2 y+1=2 \sqrt{2 x+y+6} \end{array}\right. \]
Cách giải 1:
a) Từ giả thiết, ta có \(a b+b c+c a=a b c\). Do đó
\[ \dfrac{1}{a+b c}=\dfrac{a}{a^2+a b c}=\dfrac{a}{a^2+a b+b c+c a}=\dfrac{a}{(a+b)(a+c)} \]
Từ đây, kết hợp với các biến đổi tương tự, ta được
\[ \begin{aligned} \mathrm{VT}_{(1)} & =\dfrac{1}{2}\left[\dfrac{a}{(a+b)(a+c)}+\dfrac{b}{(b+c)(b+a)}+\dfrac{c}{(c+a)(c+b)}\right] \\ & =\dfrac{a b+b c+c a}{(a+b)(b+c)(c+a)}=\dfrac{a b c}{(a+b)(b+c)(c+a)} \\ & =\sqrt{\dfrac{a}{(a+b)(a+c)} \cdot \dfrac{b}{(b+c)(b+a)} \cdot \dfrac{c}{(c+a)(c+b)} \cdot a b c} \\ & =\sqrt{\dfrac{a b c}{(a+b c)(b+c a)(c+a b)}} \end{aligned} \]
b) Điều kiện: \(2 x+y+6 \geq 0\). Hệ phương trình đã cho tương đương với
\[ \left\{\begin{array}{l} (x+y)(2 x+y)=6 \\ (x+y)+(2 x+y)+1=2 \sqrt{2 x+y+6} \end{array}\right. \]
Đặt \(a=x+y\) và \(b=2 x+y\), khi đó ta có
\[ \left\{\begin{array}{l} a b=6 \\ a+b+1=2 \sqrt{b+6} \end{array}\right. \]
Thay \(a=\dfrac{6}{b}\) từ phương trình thứ nhất vào phương trình thứ hai, ta được \(b+\dfrac{6}{b}+1=2 \sqrt{b+6}\), hay \(b^2+b+6=2 b \sqrt{b+6}\). Một cách tương đương, ta có \((b-\sqrt{b+6})^2=0\). Giải phương trình này, ta được \(b=3\). Từ đó \(a=2\). Như vậy, ta có \(x+y=2\) và \(2 x+y=3\), suy ra \(x=y=1\). Thử lại, ta thấy thỏa mãn. Vậy, hệ phương trình đã cho có nghiệm duy nhất \((x, y)=(1,1)\).
Bài 2
(2 điểm)
1) Tìm tất cả các cặp số nguyên dương \((x, y)\) thỏa mãn đẳng thức
\[ (x+y)(5 x+y)^3+x y^3=(5 x+y)^3+x^2 y^3+x y^4 \]
2) Với \(a, b, c\) là những số thực dương thỏa mãn các điều kiện sau:
\[ \left\{\begin{array}{cc} c \leq b<\mathrm{a} \leq 3, \quad b^2+2 a \leq 10, \quad b^2+2 a+2 c \leq 14, \\ \left(a^2+1\right)\left(b^2+1\right)+4 a b \leq 2 a^3+2 b^3+2 a+2 b . \end{array}\right. \]
Tìm giá trị lớn nhất của biểu thức
\[ P=4 a^2+b^4+2 b^2+4 c^2 \]
Cách giải 1:
a) Phương trình đã cho tương đương với
\[ (x+y-1)\left[(5 x+y)^3-x y^3\right]=0 \]
Vì \(x+y-1>0\) nên từ đây, ta có \((5 x+y)^3=x y^3\). Suy ra \(x\) là số lập phương. Đặt \(x=a^3\) với \(a\) nguyên dương thì ta có \(5 a^3+y=a y\), hay \(y(a-1)=5 a^3\). Suy ra \(5 a^3\) chia hết cho \(a-1\), từ đó \(5=5 a^3-5\left(a^3-1\right)\) chia hết cho \(a-1\). Suy ra \(a-1 \in\{1,5\}\), hay \(a \in\{2,6\}\).
- Với \(a=2\), ta có \(y=40\). Một cách tương ứng, ta được \((x, y)=(8,40)\).
- Với \(a=6\), ta có \(y=216\). Một cách tương ứng, ta được \((x, y)=(216,216)\).
Vậy có hai cặp số nguyên dương \((x, y)\) thỏa mãn yêu cầu đề bài là \((8,40)\) và \((216,216)\).
b) Giả thết \(\left(a^2+1\right)\left(b^2+1\right)+4 a b \leq 2\left(a^3+b^3+a+b\right)\) có thể được viết lại thành
\[ \left(a^2-2 b+1\right)\left(b^2-2 a+1\right) \leq 0 \]
Vì \(a^2-2 b+1>a^2-2 a+1=(a-1)^2 \geq 0\) nên từ đây, ta có \(b^2-2 a+1 \leq 0\). Đặt \(x=2 a\), \(y=b^2+1\) và \(z=2 c\), khi đó ta có \(6 \geq x \geq y \geq 2 b \geq 2 c=z\). Từ các giả thiết, ta có \(x+y \leq 11, x+y+z \leq 15\). Ngoài ra, ta cũng có
\[ P+1=x^2+y^2+z^2 \]
Chú ý rằng
\[ \begin{aligned} 6^2+5^2 & +4^2-\left(x^2+y^2+z^2\right)=(6+x)(6-x)+(5+y)(5-y)+(4+z)(4-z) \\ & =(1+x-y)(6-x)+(1+y-z)(11-x-y)+(4+z)(15-x-y-z) \geq 0 \end{aligned} \]
Suy ra \(P+1 \leq 6^2+5^2+4^2=77\), hay \(P \leq 76\). Dấu đẳng thức xảy ra khi \(x=6, y=5\) và \(z=4\), hay \(a=3, b=c=2\). Vậy max \(P=76\).
Bài 3
(3 điểm)
Cho tam giác \(A B C\) nhọn, không cân, nội tiếp trong đường tròn \((O)\). Điểm \(P\) nằm trong tam giác \(A B C\). Gọi \(E, F\) lần lượt là hình chiếu vuông góc của \(P\) trên các cạnh \(C A, A B\). Giả sử tứ giác \(B C E F\) nội tiếp trong đường tròn \((K)\).
1) Chứng minh rằng \(A P\) vuông góc \(B C\).
2) Chứng minh rằng \(A P=2 O K\).
3) Đường thẳng qua \(P\) vuông góc với \(A P\) cắt đường tròn \((O)\) tại hai điểm \(Q\) và \(R\). Chứng minh rằng đường tròn tâm \(A\) bán kính \(A P\) tiếp xúc với đường tròn ngoại tiếp tam giác \(K Q R\).
Cách giải 1:
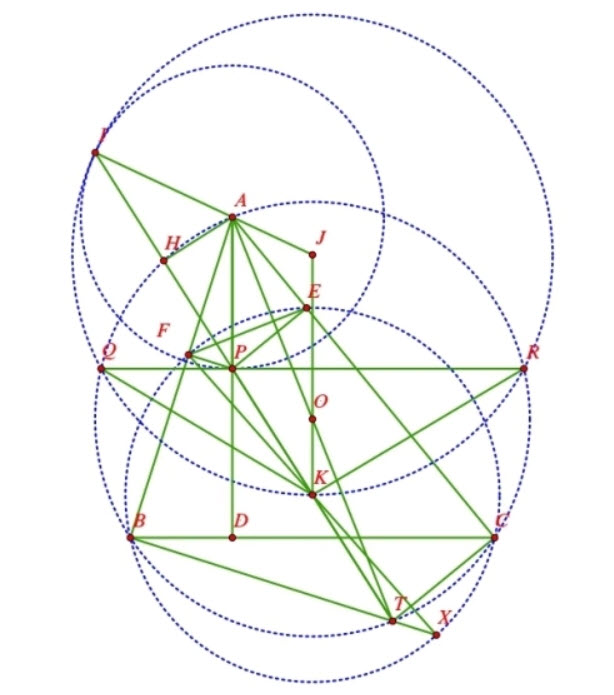
a) Gọi \(D\) là giao điểm của hai đường thẳng \(A P\) và \(B C\). Do \(\angle A E P=\angle A F P=\) \(90^{\circ}\) nên tứ giác \(A E P F\) nội tiếp, suy ra \(\angle A P E=\angle A F E\). Mà tứ giác \(B F E C\) nội tiếp nên \(\angle A C B=\angle A F E\), dẫn đến \(\angle A P E=\angle A C B\). Suy ra tứ giác \(C D P E\) nội tiếp, từ đó \(\angle A D C=\angle A E P=90^{\circ}\). Tữ đây, ta suy ra \(A P \perp B C\).
b) Gọi \(T\) và \(X\) lần lượt là các điểm đối xứng với các điểm \(P\) và \(F\) qua điểm \(K\). Ta có \(K X=K F=K B\) nên \(\angle F B X=90^{\circ}\), từ đó \(B X \| F P\). Mà \(K\) là trung điểm của các đoạn thẳng \(F X\) và \(P T\) nên \(T X \| F P\), suy ra ba điểm \(B, T, X\) thẳng hàng. Do đó \(\angle A B T=90^{\circ}\). Tương tự, ta có \(\angle A C T=90^{\circ}\). Vì vậy \(A T\) là đường kính của đường tròn \((O)\), hay \(O\) là trung điểm của đoạn \(A T\). Do \(O\) và \(K\) lần lượt là trung điểm của các đoạn thẳng \(T A\) và \(T P\) nên \(A P=2 O K\).
c) Do \(A P \perp B C, Q R \perp A P\) nên \(Q R \| B C\), mà \(O K\) là trung trực của đoạn thẳng \(B C\) nên \(O K \perp Q R\). Từ đó suy ra \(O K\) là trung trực của đoạn thẳng \(Q R\).
Gọi \(H\) là giao điểm thứ hai của đường thẳng \(T P\) và đường tròn \((O)\); \(I\) là giao điểm thứ hai của đường thẳng \(T P\) và đường tròn \((J)\) ngoại tiếp tam giác \(K Q R\).
Ta có các tứ giác \(H Q T R\) và \(K Q I R\) nội tiếp nên \(P Q \cdot P R=P H \cdot P T\) và \(P Q \cdot P R=P K \cdot P I\). Mà \(P T=2 P K\) nên ta có \(P I=2 P H\), hay \(H\) là trung điểm của đoạn thẳng \(P I\).
Lại có \(\angle A H T=90^{\circ}\) nên \(A I=A P\). Do \(A P \| K J\) nên \(\angle A P I=\angle J K I\), dẫn đến \(\angle A I P=\angle J I K\), suy ra ba điểm \(I, A, J\) thẳng hàng. Do \(I\) thuộc đường tròn \((A, A P)\) và \((J)\), đồng thời ba điểm \(I, A, J\) thẳng hàng, nên đường tròn \((A, A P)\) tiếp xúc với đường tròn \((J)\) tại \(I\). Ta có điều phải chứng minh.
Cách giải 2: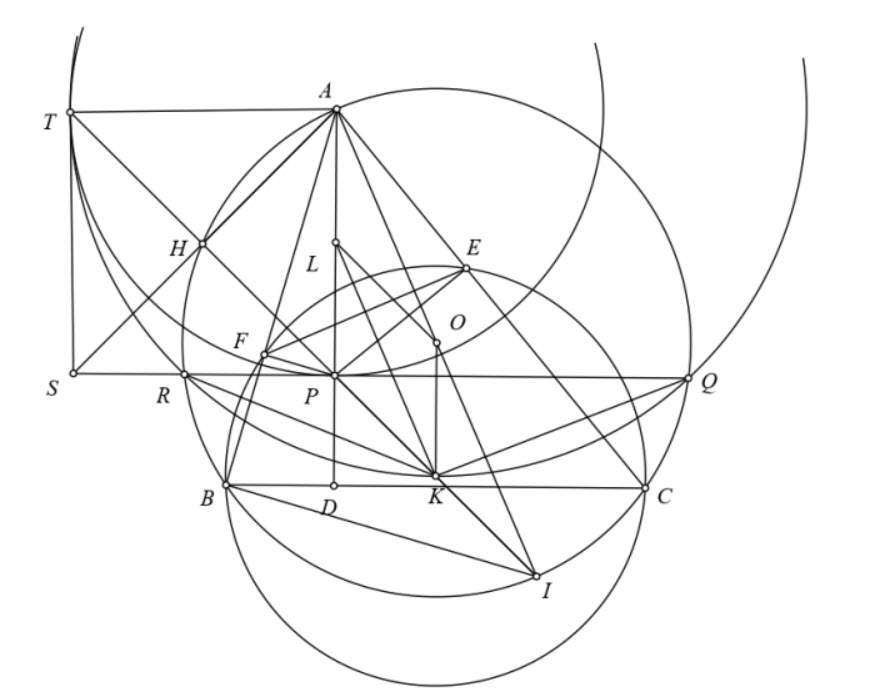
a) Gọi \(D\) là giao điểm của các đường thẳng \(A P\) và \(B C, L\) là trung điểm của đoạn thẳng \(A P\). Do \(\angle A E P=\angle A F P=90^{\circ}\) nên bốn điểm \(A, E, P, F\) cùng thuộc đường tròn \((L)\) với đường kính \(A P\).
Từ các tứ giác nội tiếp \(A E P F, B C E F\), ta có \(\angle A P E=\angle A F E=\angle B C E=\angle D C E\). Suy ra tứ giác \(C D P E\) nội tiếp. Do đó \(\angle P D C=180^{\circ}-\angle P E C=90^{\circ}\). Vì thế, \(A P \perp B C\) tại \(D\).
b) Kẻ đường kính \(A I\) của đường tròn \((O)\). Chú ý rằng tứ giác \(B C E F\) nội tiếp, ta có
\[ \angle I A E+\angle A E F=\angle I B C+\angle F B C=\angle A B I=90^{\circ} \]
Suy ra \(A I \perp E F\). Theo tính chất đường nối tâm của hai đường tròn \((K)\) và \((L)\), ta thấy \(K L \perp E F\). Do đó, \(A I \| K L\). Lại có \(A P \| O K\) (cùng vuông góc với \(B C\) ) nên \(A O K L\) là hình bình hành. Suy ra \(O K=A L=\dfrac{1}{2} A P\) hay \(A P=2 O K\).
c) Do \(A O K L\) là hình bình hành nên \(O K \| A L\) và \(O K=A L\). Vî thế, ta có \(O K \| L P\) và \(O K=L P\). Suy ra \(O K P L\) là hình bình hành. Do đó, \(O L \| P K\). Mà \(O L \| P I\) (do \(O L\) là đường trung bình của tam giác \(A P I\) ) nên ba điểm \(P, K, I\) thẳng hàng và \(P K=O L=\dfrac{1}{2} P I\). Do vậy, \(K\) là trung điểm của \(P I\).
Gọi \(H\) là giao điểm thứ hai của \(P I\) với \((O), S\) là giao điểm của \(A H\) và \(Q R, T\) là điểm đối xứng với \(P\) qua \(H\). Ta thấy \(A H \perp P T\) và \(H\) là trung điểm của \(P T\) nên \(A S\) là đường trung trực của \(P T\). Suy ra \(S P=S T, A P=A T\). Từ đó, \(T\) thuộc đường tròn \((A ; A P)\) và hai tam giác \(A P S, A T S\) bằng nhau \((\mathrm{c}-\mathrm{c}-\mathrm{c})\). Suy ra \(\angle S T A=\angle S P A=90^{\circ}\). Do đó, \(S T\) là tiếp tuyến của đường tròn \((A, A P)\).
Do tứ giác \(I Q H R\) nội tiếp và \(K, H\) lần lượt là trung điểm của \(P I, P T\), ta có
\[ P T \cdot P K=2 P H \cdot \dfrac{1}{2} P I=P H \cdot P I=P Q \cdot P R \text {. } \]
Suy ra tứ giác \(K Q T R\) nội tiếp. Áp dụng hệ thức lượng trong tam giác vuông \(A S T\) với chú ý bốn điểm \(A, H, Q, R\) cùng thuộc một đường tròn, ta có \(S T^2=S A \cdot S H=S Q \cdot S R\). Suy ra \(S T\) là tiếp tuyến của đường tròn \((T Q R)\). Hai đường tròn \((A, A P)\) và \((K Q R)\) có chung điểm \(T\) và tiếp tuyến \(S T\) nên chúng tiếp xúc nhau tại \(T\).
Bài 4
(1 điểm)
Cho các điểm \(A_1, A_2, \ldots, A_{30}\) theo thứ tự nằm trên một đường thẳng sao cho độ dài các đoạn \(A_k A_{k+1}\) bằng \(k\) (đơn vị dài), với \(k=1,2, \ldots, 29\). Ta tô mầu mỗi đoạn thẳng \(A_1 A_2, A_2 A_3, \ldots, A_{29} A_{30}\) bởi 1 trong 3 mầu (mỗi đoạn được tô bởi đúng 1 mầu). Chứng minh rằng với mọi cách tô mầu, ta luôn chọn được 2 số nguyên dương \(1 \leq j<i \leq 29\) sao cho hai đoạn \(A_i A_{i+1}, A_j A_{j+1}\) được tô cùng mầu và \(i-j\) là bình phương của số nguyên dương.
Cách giải 1:
Với mỗi \(1 \leq i \leq 29\), ta tô màu số \(i\) bởi màu tô cho đoạn \(A_i A_{i+1}\). Bài toán trở thành: Tô màu 29 số nguyên dương đầu tiên bởi 1 trong 3 màu xanh, đỏ, vàng, mỗi số đúng 1 màu. Khi đó tồn tại hai số \(i, j\) cùng màu với \(i>j\) thỏa mãn \(i-j\) là số chính phương.
Giả sử ngược lại, tồn tại cách tô màu sao cho \(i-j\) không là số chính phương với mọi số \(i, j\) cùng màu. Xét ba số \(1,10,26\), ba số này đôi một có hiệu là số chính phương \((9,16,25)\) nên chúng có màu đôi một khác nhau. Tương tự với ba số \(1,17,26\). Suy ra 10 và 17 có cùng màu, giả sử 10 và 17 đều màu đỏ.
Làm tương tự ta có 11 và 18 cùng màu (xét hai bộ số \((2,11,27)\) và \((2,18,27)\) ); 12 và 19 cùng màu (xét hai bộ số \((3,12,28),(3,19,28)\) ); 13 và 20 cùng màu (xét hai bộ số \((4,13,29)\) và \((4,20,29))\).
Ta có \(11-10=1^2\) nên 11 và 10 khác màu, giả sử 11 tô màu xanh, thế thì 18 cũng tô màu xanh. Ta lại có \(19-18=1^2\) nên 19 không thể có màu xanh, \(19-10=3^2\) nên 19 cũng không thể có màu đỏ. Vậy suy ra 19 màu vàng và 12 cũng màu vàng.
Giờ ta lại có \(20-11=3^2\) nên 20 không thể có màu xanh như \(11,20-19=1^2\) nên 20 không thể có màu vàng như 19 . Vậy suy ra 20 phải có màu đỏ, dẫn tới 13 có màu đỏ. Điều này vô lý vì 17 và 13 đều màu đỏ và \(17-13=2^2\). Mâu thuẫn nhận được cho ta điều phải chứng minh.