Bài 1
(2 điểm)
1) Giải phương trình
\[ \sqrt{x^2+6 x+2023}+\sqrt{x+3}=\sqrt{x^2+5 x+2025}+\sqrt{5} \]
2) Giải hệ phương trình
\[ \left\{\begin{array}{l} (x+6 y)(3 x+2 y)=12, \\ 2 x^3+6 y^3+15 x^2 y+19 y^2 x+x+6 y=12 \end{array}\right. \]
Cách giải 1:
1) ÐКXĐ: \(x \geq-3\).
Phương trình đã cho tương đương với
\[ \begin{aligned} & \left(\sqrt{x^2+6 x+2023}-\sqrt{x^2+5 x+2025}\right)+(\sqrt{x+3}-\sqrt{5})=0 \\ & \Leftrightarrow \dfrac{x-2}{\sqrt{x^2+6 x+2023}+\sqrt{x^2+5 x+2025}}+\dfrac{x-2}{\sqrt{x+3}+5}=0 \\ & \Leftrightarrow(x-2)\left(\dfrac{1}{\sqrt{x^2+6 x+2023}+\sqrt{x^2+5 x+2025}}+\dfrac{1}{\sqrt{x+3}+5}\right)=0 \\ & \Leftrightarrow x=2(t m) \\ & \quad\left(\text { vì } \dfrac{1}{\sqrt{x^2+6 x+2023}+\sqrt{x^2+5 x+2025}}+\dfrac{1}{\sqrt{x+3}+5}>0\right) \end{aligned} \]
Vậy phương trình đã cho có nghiệm duy nhất \(x=2\).
2) Thế phương trình (1) vào (2) ta có
\[ 2 x^3+6 y^3+15 x^2 y+19 x y^2+x+6 y=(x+6 y)(3 x+2 y) \]
Phương trình tương đương với
\[ (x+6 y)\left(2 x^2+3 x y+y^2\right)+(x+6 y)=(x+6 y)(3 x+2 y) \]
Từ phương trình (1) ta suy ra \(x+6 y \neq 0\). Do đó
\[ 2 x^2+3 x y+y^2+1=3 x+2 y \]
Suy ra
\[ (2 x+y)(x+y)+1=(x+y)+(2 x+y) \Leftrightarrow(x+y-1)(2 x+y-1)=0 \]
Xét các trường hợp:
- Nếu \(2 x+y=1\) thay vào phương trình (1) ta có
\[ (6-11 x)(2-x)=12 \]
Giải phương trình trên ta thu được \(x=0\) hoặc \(x=\dfrac{28}{11}\). Từ đó ta thu được hai nghiệm \((0,1)\) và \(\left(\dfrac{28}{11}, \dfrac{-45}{11}\right)\)
- Nếu \(x+y=1\) thay vào phương trình (1) ta có
\[ (1+5 y)(3-y)=12 \]
Giải phương trình trên ta thu được \(y=1\) hoặc \(y=\dfrac{9}{5}\). Từ đó ta thu được hai nghiệm của hệ là \((0,1)\) và \(\left(\dfrac{-4}{5}, \dfrac{9}{5}\right)\).
Bài 2
(2 điểm)
1) Giả sử \(n\) là số nguyên sao cho \(3 n^3-1011\) chia hết cho 1008 . Chứng minh rằng \(n-1\) chia hết cho 48.
2) Với \(a, b, c\) là các số dương thỏa mãn điều kiện \(a b+b c+c a=1\). Chứng minh rằng
\[ \left(1+\dfrac{1}{1+a^2}\right)\left(1+\dfrac{1}{1+b^2}\right)\left(1+\dfrac{1}{1+c^2}\right)>4 \]
Cách giải 1:
1. Ta có: \(3 n^3-1011=3\left(n^3-337\right)=1008 k\left(k \in N^*\right)\) nên \(n^3-337=336 k\), dẫn đến
\[ n^3-1=336(k+1) \]
hay
\[ (n-1)\left(n^2+n+1\right)=48 \cdot 7 k \]
Do \(n^2+n+1\) là số lẻ nên \(n^2+n+1\) không chia hết cho 16 .
Bởi vậy \(n-1\) chia hết cho 16 . (1)
Thêm nữa, nếu \(n \equiv 0 ; 2(\bmod 3) \Leftrightarrow n^2+n+1 \equiv 1(\bmod 3) \Rightarrow n-1: 3\)
Nếu \(n \equiv 1(\bmod 3) \Leftrightarrow n-1: 3\)
Vậy \(n-1: 3\) (2)
Từ \((1)\) và \((2) \Rightarrow\) ĐPCM.
2. Bất đẳng thức cần chứng minh tương đương với:
\[ \left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)>4\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right) \]
Khai triển và rút gọn, BDT này tương đương với:
\[ 3 a^2 b^2 c^2+2\left(a^2 b^2+b^2 c^2+c^2 a^2\right)<4 \]
Mặt khác, vì \(a b+b c+c a=1\), ta có:
- \(a^2 b^2+b^2 c^2+c^2 a^2<(a b+b c+c a)^2=1\).
- \(a^2 b^2 c^2 \leq \dfrac{(a b+b c+c a)^3}{27}=\dfrac{1}{27}\).
Do đó, \(V T_{(1)}<\dfrac{1}{9}+2<4\). Ta có điều cần chứng minh.
Bài 3
(3 điểm)
Cho hai đường tròn \((O)\) và \(\left(O^{\prime}\right)\) cố định cắt nhau tại \(A\) và \(B\) sao cho \(O\) nằm ngoài \(\left(O^{\prime}\right)\) và \(O^{\prime}\) nằm ngoài \((O)\). Trên đường tròn \((O)\) lấy điểm \(P\) di chuyển sao cho \(P\) nằm trong đường tròn \(\left(O^{\prime}\right)\). Đường thẳng \(A P\) cắt \(\left(O^{\prime}\right)\) tại \(C\) khác \(A\).
(1)) Chứng minh rằng hai tam giác \(O B P\) và \(O^{\prime} B C\) dồng dạng.
2) Gọi \(Q\) là giao điểm của hai đường thẳng \(O P\) và \(O^{\prime} C\). Chứng minh rằng \(\widehat{Q B C}+\widehat{A B P}=90^{\circ}\).
3) Lấy điểm \(D\) thuộc \((O)\) sao cho \(A D\) vuông góc \(O^{\prime} C\). Chứng minh rằng trung điểm của đoạn thẳng \(D Q\) luôn nằm trên một đường tròn cố định khi \(P\) thay đổi.
Cách giải 1:
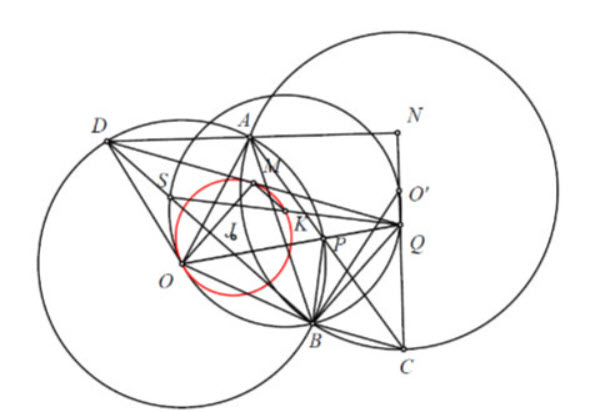
1. Ta có \(\angle P O B=2 \angle P A B=\angle B O^{\prime} C\) nên hai tam giác \(O B P\) và \(O^{\prime} B C\) dồng dạng.
2. Từ câu 1) ta thu được \(\angle O P B=\angle O^{\prime} C B\) nên tứ giác \(B P Q C\) nội tiếp. Suy ra \(\angle Q B C=\) \(\angle Q P C=\angle A P O=90^{\circ}-\dfrac{1}{2} \angle A O P=90^{\circ}-\angle A B P\).
3. \(C Q\) cắt \(A D\) tại \(N . M\) là trung điểm của \(D Q\).
Ta có \(\angle B Q C=\angle B P C=\angle B A N\) nên tứ giác \(D N Q B\) nội tiếp.
Suy ra \(\angle D B Q=90^{\circ}\).
Suy ra \(M D=M B=M Q\), ta thu được \(O M \perp B D\).
Từ câu 1) ta cũng có \(\angle B O Q=\angle B O^{\prime} Q\) nên tứ giác \(B O O^{\prime} Q\) nội tiếp \((K)\).
Kẻ đường kính \(Q S\) của \((K)\) thì \(D, S, B\) thẳng hàng.
Ta có \(M K \| D S\) nên \(\angle O M K=90^{\circ}\). Do \(O, B, O^{\prime}\) cố định nên \(K\) cố định.
Vậy \(M\) chuyển động trên đường tròn đường kính \(O K\) cố định.
Bài 4
(1 điểm)
Giả sử \(A\) là tập hợp con của tập hợp gồm 30 số tự nhiên đầu tiên \(\{0,1,2,3, \ldots, 29\}\) sao cho với \(k\) nguyên bất kỳ, \(a, b \in A\) bất kỳ (có thể \(a=b\) ) thì \(a+b+30 k\) không là tích của hai số nguyên liên tiếp. Chứng minh rằng số phần tử của tập hợp \(A\) nhỏ hơn hoặc bằng 10.
Cách giải 1:
Giả sử \(A\) là tập hợp con của tập hợp gồm 30 số tự nhiên đầu tiên \(\{0,1,2, \cdots, 29\}\) sao cho với \(k\) nguyên bất kỳ, \(a, b \in A\) bất kỳ (có thể \(a=b\) ) thì \(a+b+30 k\) không là tích của hai số nguyên liên tiếp. Chứng minh rằng số phần tử của tập hợp \(A\) nhỏ hơn hoặc bằng 10 .
Chứng \(\operatorname{minh}\). Nhận xét: nếu \(n\) nguyên thì \(n(n+1) \equiv 0,2,6,12,20,26(\bmod 30)\). Do đó, nếu
\[ a \in X=\{0,1,3,6,10,13,15,16,18,21,25,28\} \]
thì \(2 a \equiv 0,2,6,12,20,26(\bmod 30)\). Do đó, luôn tồn tại \(k, n\) nguyên để
\[ 2 a+30 k=n(n+1) \]
Vậy, tập \(A\) không chứa phần tử nào của tập \(X\).
Mặt khác, nếu \((a, b) \in\{(2,4),(5,7),(8,12),(9,11),(19,23),(20,22),(24,26),(27,29)\}\) thì
\[ a+b \equiv 0,2,6,12,20,26 \quad(\bmod 30) \]
Khi đó cung tồn tại \(k, n\) nguyên để
\[ a+b+30 k=n(n+1) \]
Như vậy, mỗi nhóm ở trên có tối đa 1 số thuộc \(A\). Từ đây suy ra tập A có không quá 10 số.
Chú ý. Ta cũng có thể chứng minh 10 là số phần tử nhiều nhất có thể của tập \(A\). Thật vậy, lấy
\[ A=\{2,5,8,11,14,17,20,23,26,29\} \]
thì với \(a, b\) bất kì thuộc \(A, a+b \equiv 1(\bmod 3)\). Khi đó \(a+b+30 k \not \equiv 0,2,6,12,20,26(\bmod 30)\).