Bài 1
(2 điểm)
1) Giải phương trình
\[ 2 x+1+2 \sqrt{4 x^2+6 x}=4 \sqrt{5 x-x^2} \]
2) Giải hệ phương trình
\[ \left\{\begin{array}{l} x y(x+y)=30 \\ x^3+y^3=30+\sqrt[3]{x+y+120} \end{array}\right. \]
Cách giải 1:
a) Điều kiện: \(0 \leq x \leq 5\). Phương trình đã cho tương đương với
\[ (4 x+6)+x+2 \sqrt{4 x^2+6 x}=4 x+(5-x)+4 \sqrt{5 x-x^2} \]
hay
\[ (\sqrt{4 x+6}+\sqrt{x})^2=(2 \sqrt{x}+\sqrt{5-x})^2 \]
Từ đó \(\sqrt{4 x+6}+\sqrt{x}=2 \sqrt{x}+\sqrt{5-x}\), hay \(\sqrt{4 x+6}=\sqrt{x}+\sqrt{5-x}\). Phương trình này tương đương với \(4 x+6=5+2 \sqrt{5 x-x^2}\), hay
\[ 4 x+1=2 \sqrt{5 x-x^2} \]
Bình phương hai vế rồi rút gọn, ta được \((10 x-1)(2 x-1)=0\). Suy ra \(x=\dfrac{1}{10}\) hoặc \(x=\dfrac{1}{2}\). Thử lại, ta thấy đều thỏa mãn. Vậy, phương trình đã cho có hai nghiệm là \(x=\dfrac{1}{2}\) và \(x=\dfrac{1}{10}\).
b) Phương trình thứ hai của hệ có thể được viết lại thành
\[ (x+y)^3+(x+y)=x+y+30+3 x y(x+y)+\sqrt[3]{x+y+120} \]
Kết hợp với phương trình thứ nhất của hệ, ta được
\[ (x+y)^3+(x+y)=x+y+120+\sqrt[3]{x+y+120} \]
Từ đây, dễ thấy \(x+y=\sqrt[3]{x+y+120}\). Giải phương trình với ẩn \(x+y\), ta được \(x+y=5\). Thay vào phương trình thứ nhất của hệ, ta được \(x y=6\). Giải hệ phương trình \(x+y=5\) và \(x y=6\), ta tìm được các nghiệm \((x, y)\) của hệ phương trình đã cho là \((3,2)\) và \((2,3)\).
Bài 2
(2 điểm)
1) Tìm tất cả các cặp số nguyên dương \((x ; y)\) thỏa mãn
\[ 4^x+\left(1+3^y\right)\left(1+7^y\right)=2^x\left(3^y+7^y+2\right) \]
2) Với \(x, y, z\) là những số thực dương, tìm giá trị nhỏ nhất của biểu thức:
\[ M=\dfrac{x^{14}-x^6+3}{x^2 y^2+z x+z y}+\dfrac{y^{14}-y^6+3}{y^2 z^2+x y+x z}+\dfrac{z^{14}-z^6+3}{z^2 x^2+y z+y x} \]
Cách giải 1:
a) Phương trình đã cho có thể được viết lại thành \(\left(2^x-3^y-1\right)\left(2^x-7^y-1\right)=0\). Từ đó \(2^x=3^y+1\) hoặc \(2^x=7^y+1\).
Trường hợp 1: \(2^x=3^y+1\). Giả sử \(x \geq 3\), khi đó từ phương trình ta suy ra \(3^y+1\) chia hết cho 8 , tức \(3^y\) chia 8 dư 7 . Tuy nhiên, bằng kiểm tra trực tiếp, ta dễ thấy \(3^y\) chỉ có thể chia \(8 \mathrm{dư}\) 1 hoặc 3 mà thôi. Từ mâu thuẫn này, ta suy ra \(x \leq 2\). Thử trực tiếp, ta được \((x, y)=(2,1)\).
Trường hợp \(2: 2^x=7^y+1\). Tự phương trình, ta suy ra \(2^x \equiv 1(\bmod 7)\). Từ đó, bằng kiểm tra trực tiếp, ta dễ thấy \(x\) phải là một bội của 3 . Đặt \(x=3 k\) với \(k\) nguyên dương, phương trình có thế được viết lại thành \((a-1)\left(a^2+a+1\right)=7^y\), trong đó \(a=2^k\). Suy ra \(a-1\) và \(a^2+a+1\) đều là lũy thừa của 7 . Mà \(a^2+a+1>a-1\) nên \(a^2+a+1\) chia hết cho \(a-1\). Vi \(a^2+a+1=(a-1)(a+2)+3\) nên 3 chia hết cho \(a-1\), mà \(a-1\) là một lũy thừa của 7 nên \(a-1=1\), tức \(a=2\). Suy ra \(k=1\), tức \(x=3\). Một cách tương ứng, ta tìm được \(y=1\). Vậy, có hai cặp số \((x, y)\) thỏa mãn yêu cầu đề bài là \((2,1)\) và \((3,1)\).
b) Chú ý rằng \(\left(x^8-1\right)\left(x^6-1\right) \geq 0\), do đó \(x^{14}-x^6 \geq x^8-1\). Từ đó suy ra
\[ x^{14}-x^6+3 \geq x^8+2 \geq 2 x^4+1 \]
Thiết lập các bất đẳng thức tương tự, ta được \(M \geq 2 A+B\), trong đó
\[ \begin{aligned} A & =\dfrac{x^4}{x^2 y^2+z x+z y}+\dfrac{y^4}{y^2 z^2+x y+x z}+\dfrac{z^4}{z^2 x^2+y z+y x} \\ B & =\dfrac{1}{x^2 y^2+z x+z y}+\dfrac{1}{y^2 z^2+x y+x z}+\dfrac{1}{z^2 x^2+y z+y x} \end{aligned} \]
Sử dụng bất đẳng thức Cauchy-Schwarz, kết hợp với các bất đẳng thức quen thuộc (có thể chứng minh bằng biến đổi tương đương) \(x^2 y^2+y^2 z^2+z^2 x^2 \leq \dfrac{1}{3}\left(x^2+y^2+z^2\right)^2\) và \(x y+y z+z x \leq x^2+y^2+z^2\), ta được
\[ \begin{aligned} & A \geq \dfrac{\left(x^2+y^2+z^2\right)^2}{x^2 y^2+y^2 z^2+z^2 x^2+2(x y+y z+z x)} \geq \dfrac{a^2}{\dfrac{1}{3} a^2+2 a}=\dfrac{3 a^2}{a(a+6)} \\ & B \geq \dfrac{9}{x^2 y^2+y^2 z^2+z^2 x^2+2(x y+y z+z x)} \geq \dfrac{9}{\dfrac{1}{3} a^2+2 a}=\dfrac{27}{a(a+6)} \end{aligned} \]
trong đó \(a=x^2+y^2+z^2\). Suy ra
\[ M \geq \dfrac{6 a^2}{a(a+6)}+\dfrac{27}{a(a+6)}=\dfrac{3\left(2 a^2+9\right)}{a^2+6 a} \geq \dfrac{3\left(2 a^2+9\right)}{a^2+\left(a^2+9\right)}=3 \]
Mặt khác, dễ thấy với \(x=y=z=1\), thì \(M=3\). Vậy \(\min M=3\).
Bài 3
(3 điểm)
Cho tam giác \(A B C\) nhọn với \(A B \lt A C\) nội tiếp trong đường tròn \((O)\) có tiếp tuyến tại \(A\) của \((O)\) cắt \(B C\) ở \(T\) sao cho \(T B>B C\). Gọi \(P\) và \(E\) lần lượt là trung điểm của \(T A\) và \(T C\).
1) Chứng minh rằng tứ giác \(A P E B\) nội tiếp.
2) Gọi giao điểm thứ hai của \(A E\) với \((O)\) là \(F\). Lấy \(G\) thuộc \((O)\) sao cho \(F G\) song song với \(A C\). Chứng minh rằng \(\widehat{A T G}=\widehat{T A F}\).
3) Gọi \(H\) là trực tâm của tam giác \(A B C, D\) là giao điểm của \(A H\) và \(B C . M\) là trung điểm \(B C\). K đối xứng với \(A\) qua \(B C\). \(N\) thuộc đường thẳng \(A M\) sao cho \(K N\) song song với \(H M\). Lấy \(S\) thuộc \(B C\) sao cho \(N S \perp N K\). Dựng \(R\) thuộc tia \(A K\) sao cho \(A R \cdot A H=A D^2\). \(Q\) là điểm sao cho \(P Q \perp A S\) và \(S Q \perp A O\). Chứng minh rằng điểm đối \(A R \cdot A H=A D \cdot Q\) uúng của \(A\) qua \(Q R\) thuộc đường tròn đường kính \(D N\). xứng của \(A\) qua \(Q R\) thuộc đường tròn đường kính \(D N\).
Cách giải 1:
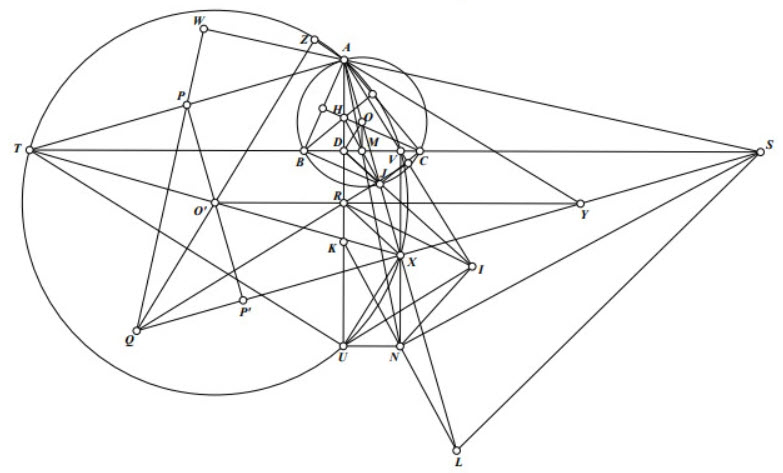
Gọi AJ là đường kính của \((\mathrm{O})\). Ta có BHCJ là hình bình hành nên M là trung điểm HJ . Gọi AJ cắt KN tại L . Do M là trung điểm HJ và \(\mathrm{HJ} / / \mathrm{KL}\) nên N là trung điểm KL . Mà \(\mathrm{NS} \perp \mathrm{NK}\) nên \(\mathrm{SL}=\mathrm{SK}\), mà \(\mathrm{SA}=\mathrm{SK}\) (do D là trung điểm AK ) nên \(\mathrm{SA}=\mathrm{SL}\).
Lại có: \(\mathrm{SQ} \perp \mathrm{AL}\) nên SQ là đường trung trực của AL hay SQ vuông góc AL tại trung điểm X của AL .
Gọi U đối xứng với A qua R. Ta có: \(A H \cdot A R=A D^2\) nên \(A H \cdot A U=A D \cdot A K\) \(\Rightarrow \dfrac{A M}{A N}=\dfrac{A H}{A K}=\dfrac{A D}{A U}\) nên \(\mathrm{DM} / / \mathrm{UN} \Rightarrow \mathrm{NU} \perp \mathrm{AU}\).
Ta có: NX//AK (đường trung bình) nên \(\mathrm{NX} / / \mathrm{OM}\), mà \(\mathrm{MD} / / \mathrm{NU}\) nên \(\dfrac{A O}{A X}=\dfrac{A M}{A N}=\dfrac{A D}{A U}\) nên OD//UX.
Ta có: \(A H . A U=2 A D^2\) nên \(\mathrm{OM} . \mathrm{AU}=\mathrm{AD}^2\)
Ta có tứ giác OMTA nội tiếp \((\mathrm{OT})\). Gọi \((\mathrm{OT})\) cắt AD tại \(\mathrm{A}^{\prime}\). Có: AOMA ' là hình thang cân nên \(\mathrm{DA}^{\prime}-\mathrm{DA}^{\prime}=\mathrm{DA}^{\prime}-\mathrm{AD}^{\prime}=\mathrm{DD}^{\prime}=\mathrm{OM}\).
Do DT.DM=DA'.DA=DA.(DA-OM) \(=\mathrm{DA}^2\)-DA. \(\mathrm{OM}=\mathrm{OM} \cdot \mathrm{AU}-\mathrm{DA} \cdot \mathrm{OM}=\mathrm{OM} \cdot \mathrm{DU}\) \(\Rightarrow \dfrac{D T}{D U}=\dfrac{M O}{M D}\) nên \(\triangle \mathrm{DTU} \sim \Delta \mathrm{MOD}\) (c.g.c) \(\Rightarrow \angle \mathrm{DTU}=\angle \mathrm{DOM}\) nên \(\mathrm{OD} \perp \mathrm{TU}\).
Mà \(\mathrm{OD} / / \mathrm{UX}\) nên \(\angle \mathrm{TUX}=90^{\circ}\).
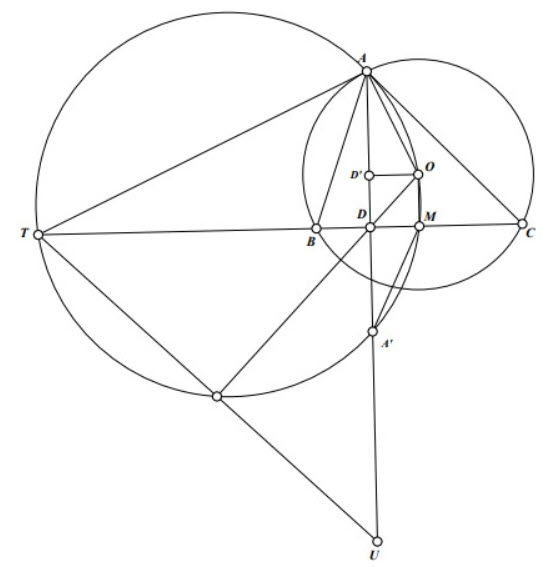
Ta có \(N X \perp B C\) tại \(V\) nên \(T, A, V, X, U\) thuộc \(\left(O^{\prime}\right)\) đường kính \(T X\).
\(\Rightarrow O^{\prime} R\) là đường trung trực của \(A U\) nên \(O^{\prime} R / / S T\) nên \(O^{\prime} R\) đi qua trung điểm \(Y\) của SX .
Gọi PO ' cắt QX tại \(\mathrm{P}^{\prime}\). Ta có: \(\mathrm{AT} / / \mathrm{XQ}\) mà \(\mathrm{O}^{\prime}\) là trung điểm TX nên \(\mathrm{O}^{\prime}\) là trung điểm \(\mathrm{PP}^{\prime}\). Ta cũng có: \(\mathrm{PO}^{\prime} / / \mathrm{AX}\) nên \(\mathrm{PP}{ }^{\prime} \perp \mathrm{XQ}\), mà \(\mathrm{PQ} \perp \mathrm{AS}\) nên \(\triangle \mathrm{P}^{\prime} \mathrm{PQ} \sim \triangle \mathrm{XSA}\) (g.g) mà \(\mathrm{O}^{\prime}, \mathrm{Y}\) là trung điểm PP ' và XS nên \(\triangle \mathrm{P}^{\prime} \mathrm{QO}^{\prime} \sim \triangle \mathrm{XAY}\) (c.g.c) nên \(\angle \mathrm{QO}^{\prime} \mathrm{P}^{\prime}=\angle \mathrm{XYA}\) nên \(\mathrm{QO}^{\prime} \perp \mathrm{AY}\) tại Z .
Suy ra YR.YO' \(=Y A . Y Z=Y X\). YQ nên tứ giác QO'RX nội tiếp.
Nên \(\angle \mathrm{O}^{\prime} \mathrm{RQ}=\angle \mathrm{O}^{\prime} \mathrm{XQ}=\angle \mathrm{XTA}=\angle \mathrm{XUA}=\angle \mathrm{VAU}\) (vì tứ giác AVXU nội tiếp và \(\mathrm{XV} / / \mathrm{AU}\) ). Mà \(\angle \mathrm{ARO}{ }^{\prime}=90^{\circ}\) nên \(\mathrm{QR} \perp \mathrm{AV}\).
Gọi I đối xứng với A qua QR thì \(\mathrm{QR} \perp \mathrm{AI}\) nên \(\mathrm{A}, \mathrm{V}, \mathrm{I}\) thẳng hàng.
Do \(\mathrm{RI}=\mathrm{RA}=\mathrm{RU}\) nên \(\angle \mathrm{AIU}=90^{\circ}\) dẫn đến \(\triangle \mathrm{ADV} \sim \Delta \mathrm{AIU}(\mathrm{g} . \mathrm{g})\)
\(\Rightarrow \dfrac{I A}{I U}=\dfrac{D A}{D V}=\dfrac{D A}{U N} \Rightarrow \dfrac{A D}{A I}=\dfrac{U N}{U I}\) mà \(\angle \mathrm{AUN}=\angle \mathrm{AIU}=90^{\circ}\) nên \(\angle \mathrm{IUN}=\angle \mathrm{IAU}\)
Từ đó \(\triangle \mathrm{ADI} \sim \Delta \mathrm{UNI}\) (c.g.c) \(\Rightarrow>\angle \mathrm{AID}=\angle \mathrm{UIN}=>\angle \mathrm{DIN}=\mathrm{AIU}=90^{\circ}\).
Bài 4
(1 điểm)
Viết một trăm số nguyên dương đầu tiên \(1,2,3, \ldots, 100\) vào một bảng ô vuông kích thước \(10 \times 10\) một cách tùy ý sao cho mỗi ô được viết đúng một số. Chứng minh rằng tồn tại hai ô kề nhau ( 2 ô có cạnh chung) mà hai số viết ở hai ô này có hiệu lớn hơn hoặc bằng 10.
Cách giải 1:
Giả sử khoảng cách của hai số được điểm ở hai ô kề nhau bất kỳ đều không vượt quá 9. Xét các số lớn nhất ở mỗi dòng và các số lớn nhất ở mỗi cột. Gọi \(m\) là số nhỏ nhất trong các số này. Không mất tính tổng quát, giả sử \(m\) là số lớn nhất ở dòng \(i\). Xét một cột \(j\) bất kỳ, gọi \(M\) là số lớn nhất ở cột này, và \(a_{i j}\) là số được điền ở ô giao giữa dòng \(i\) và cột \(j\). Ta có
\[ M \geq m \geq a_{i j} \]
Vi khoảng cách giữa hai số được điền ở hai ô kề nhau bất kỳ đều không vượt quá 9 nên trong các số ở cột \(j\), phải có một số thuộc tập hợp \(A=\{m, m+1, \ldots, m+8\}\).
Như vậy, ở mỗi cột đều có một số thuộc tập \(A\). Mà có tất cả 10 cột nên tồn tại hai số bằng nhau ở hai cột khác nhau, mâu thuẫn. Vậy, phải tồn tại hai số được điền ở hai ô kề nhau nào đó mà khoảng cách của chúng không nhỏ hơn 10 .