Bài 1
(3.5 điểm)
1) Giải phương trình
\[ \dfrac{1}{\sqrt{5 x^2+10 x+30}}+\dfrac{1}{3 \sqrt{x^2-2 x+6}}=\dfrac{1}{3 \sqrt{5}}+\dfrac{1}{\sqrt{x^4+8 x^2+36}} \]
2) Giải hệ phương trình
\[ \left\{\begin{array}{l} \left(\dfrac{1}{x}+\dfrac{1}{y}\right)(3+x y)=8, \\ \dfrac{x}{y}+\dfrac{2 y}{x}+\dfrac{1}{x}+\dfrac{1}{y}=5 \end{array}\right. \]
Cách giải 1:
a) Phương trình luôn xác định với mọi số thực \(x\). Đặt \(a=\sqrt{x^2+2 x+6}\) và \(b=\sqrt{x^2-2 x+6}\), khi đó ta có \(a b=\sqrt{x^4+8 x^2+36}\). Phương trình đã cho có thể được viết lại thành \(\dfrac{1}{\sqrt{5} a}+\dfrac{1}{3 b}=\dfrac{1}{3 \sqrt{5}}+\dfrac{1}{a b}\), hay \((a-3)(b-\sqrt{5})=0\). Từ đây, ta có \(a=3\) hoặc \(b=\sqrt{5}\). Xét từng trường hợp, ta tìm được tập nghiệm của phương trình đã cho là \(S=\{1,-3\}\).
b) Điều kiện: \(x y \neq 0\). Phương trình thứ hai có thể được viết lại \(\dfrac{x}{y}+\dfrac{2 y}{x}+\dfrac{1}{x}+\dfrac{1}{y}+3=8\), hay \(\left(\dfrac{1}{x}+\dfrac{1}{y}\right)(x+2 y+1)=8\). Kết hợp với phương trình thứ nhất của hệ, ta được
\[ x y+3=x+2 y+1 \]
hay \((x-2)(y-1)=0\). Từ đó \(x=2\) hoặc \(y=1\). Xét từng trường hợp, ta tìm được tất cả các nghiệm \((x, y)\) của hệ phương trình đã cho là \((1,1),(3,1),\left(2, \dfrac{9-\sqrt{33}}{4}\right),\left(2, \dfrac{9+\sqrt{33}}{4}\right)\).
Bài 2
(2.5 điểm)
1) Tìm các số nguyên dương \(x, y, z\) thỏa mãn hệ phương trình
\[ \left\{\begin{array}{l} 27 x^3+27 x^2+10 y=(x+3 z)^3 \\ 27 y^3+27 y^2+10 x=(y+3 z)^3 \end{array}\right. \]
2) Với \(a, b, c\) là các số thực dương thỏa mãn điều kiện
\[ (a+2) b^2+(b+2) c^2+(c+2) a^2 \geq 8+a b c \]
Chứng minh rằng
\[ 2(a b+b c+c a) \leq a^2(a+b)+b^2(b+c)+c^2(c+a) \]
Cách giải 1:
a) Không mất tính tổng quát, giả sử \(x \geq y\). Từ giả thiết, ta có \(27 x^3+27 x^2+10 y\) là số lập phương. Mặt khác, ta lại có
\[ (3 x)^3=27 x^3<27 x^3+27 x^2+10 y \leq 27 x^3+27 x^2+10 x \leq 27 x^3+27 x^2+10 x<(3 x+2)^3 \]
nên \(27 x^3=27 x^2+10 y=(3 x+1)^3\), hay \(10 y=9 x+1\). Khi đó, ta có
\[ 27 y^3+27 y^2+10 x=27 y^3+27 y^2+\dfrac{100 y-10}{9} \]
Theo giả thiết thì \(27 y^3+27 y^2+10 x\) là số lập phương nên \(27 y^3+27 y^2+\dfrac{100 y-10}{9}\) là số lập phương. Mặt khác, ta lại có
\[ (3 y)^3<27 y^3+27 y^2+\dfrac{100 y-10}{9}<(3 y+2)^3 \]
nên \(27 y^3+27 y^2+\dfrac{100 y-10}{9}=(3 y+1)^3\), hay \(y=1\). Kết hợp với \(10 y=9 x+1\), ta được \(x=1\). Thay trở lại giả thiết, ta tìm được ngay \(z=1\). Vậy, có duy nhất một bộ số \((x, y, z)\) thỏa mãn yêu cầu đề bài là \((1,1,1)\).
b) Giả thiết của bài toán có thể được viết lại thành
\[ 8 \leq 2\left(a^2+b^2+c^2\right)+\left(a b^2+b c^2+c a^2-a b c\right) \]
Không mất tính tổng quát, giả sử \(b\) nằm giữa \(a\) và \(c\). Khi đó, ta có \(a(b-c)(b-a) \leq 0\). Suy ra \(a b^2+c a^2 \leq a b c+a^2 b\). Từ đây, kết hợp với bất đẳng thức AM-GM, ta có
\[ \begin{aligned} a b^2+b c^2+c a^2-a b c & \leq b\left(a^2+c^2\right)=\sqrt{b^2\left(a^2+c^2\right)^2}=2 \sqrt{b^2 \cdot \dfrac{a^2+c^2}{2} \cdot \dfrac{a^2+c^2}{2}} \\ & \leq 2 \sqrt{\left(\dfrac{b^2+a^2+c^2}{3}\right)^3} \end{aligned} \]
Kết hợp với giả thiết (1), ta được
\[ 8 \leq 2\left(a^2+b^2+c^2\right)+2 \sqrt{\left(\dfrac{a^2+b^2+c^2}{3}\right)^3} \]
Từ đó, ta dễ dàng suy ra \(a^2+b^2+c^2 \geq 3\). Kết hợp với các bất đẳng thức phụ quen thuộc \(a b+b c+c a \leq \dfrac{1}{3}(a+b+c)^2\) và \(a b+b c+c a \leq a^2+b^2+c^2\), ta được
\[ \begin{aligned} 2(a b+b c+c a) & =2 \sqrt{a b+b c+c a} \sqrt{a b+b c+c a} \\ & \leq 2 \sqrt{\dfrac{1}{3}(a+b+c)^2} \sqrt{a^2+b^2+c^2} \sqrt{\dfrac{a^2+b^2+c^2}{3}} \\ & =\dfrac{2}{3}(a+b+c)\left(a^2+b^2+c^2\right) \end{aligned} \]
Như vậy, để chứng minh bất đẳng thức đã cho, ta chỉ cần chứng minh
\[ a^2(a+b)+b^2(b+c)+c^2(c+a) \geq \dfrac{2}{3}(a+b+c)\left(a^2+b^2+c^2\right) \]
Bất đẳng thức này tương đương với
\[ a^3+b^3+c^3+a^2 b+b^2 c+c^2 a \geq 2 a b^2+2 b c^2+2 c a^2 \]
hay
\[ b(a-b)^2+c(b-c)^2+a(c-a)^2 \geq 0 \]
Bất đẳng thức cuối hiển nhiên đúng. Từ đây, ta có điều phải chứng minh.
Bình luận. Một cách khác để làm ý b) của bài toán là biến đổi giả thiết thành
\[ \dfrac{a}{b+2}+\dfrac{b}{c+2}+\dfrac{c}{a+2} \geq 1 \]
Chứng minh điều này rất đơn giản, ta chỉ cần sử dụng biến đổi tương đương là được. Bây giờ, sử dụng bất đẳng thức Cauchy-Schwarz, ta được
\[ \dfrac{a}{b+2}=\dfrac{a\left(b+c^2+a^2\right)}{(b+1+1)\left(b+c^2+a^2\right)} \leq \dfrac{a\left(b+c^2+a^2\right)}{(a+b+c)^2} \]
Thiết lập các bất đẳng thức tương tự rồi cộng lại, sau đó sử dụng bất đẳng thức (2), ta được
\[ \begin{aligned} 1 & \leq \dfrac{a\left(b+c^2+a^2\right)+b\left(c+a^2+b^2\right)+c\left(a+b^2+c^2\right)}{(a+b+c)^2} \\ & =\dfrac{a b+b c+c a+a^2(a+b)+b^2(b+c)+c^2(c+a)}{(a+b+c)^2} \end{aligned} \]
Từ đó suy ra \((a+b+c)^2 \leq a b+b c+c a+a^2(a+b)+b^2(b+c)+c^2(c+a)\), hay
\[ a^2(a+b)+b^2(b+c)+c^2(c+a) \geq a^2+b^2+c^2+a b+b c+c a \]
Mà \(a^2+b^2+c^2 \geq a b+b c+c a\) nên
\[ a^2(a+b)+b^2(b+c)+c^2(c+a) \geq 2(a b+b c+c a) \]
Đây chính là bất đẳng thức cần chứng minh.
Cách này tuy đơn giản nhưng việc nghĩ ra biến đổi giả thiết thành bất đẳng thức (2) là một điều hết sức không tự nhiên. Vî vậy, trong lời giải, chúng tôi chọn trình bày cách như ở trên.
Bài 3
(3 điểm)
Cho hình vuông \(A B C D\). Lấy điểm \(P\) thuộc cạnh \(A B\) ( \(P\) khác \(A\) và \(B\) ). Gọi \(J\) là tâm đường tròn nội tiếp của tam giác \(P A D\).
1) Chứng minh rằng tứ giác \(P J D B\) nội tiếp.
2) Gọi \(H\) là trực tâm của tam giác \(P J D, S\) là giao điểm của \(J H\) và \(A D\). Chứng minh rằng \(S H=S D\).
3) Gọi \(L\) là tâm đường tròn nội tiếp của tam giác \(P B C, K\) là trực tâm của tam giác \(L P C\). Đường tròn nội tiếp của tam giác \(P C D\) tiếp xúc \(C D\) tại \(E\). Lấy \(F\) thuộc đoạn thẳng \(C D\) sao cho \(C F=D E\). Chứng minh rằng tam giác \(F H K\) vuông cân.
Cách giải 1:
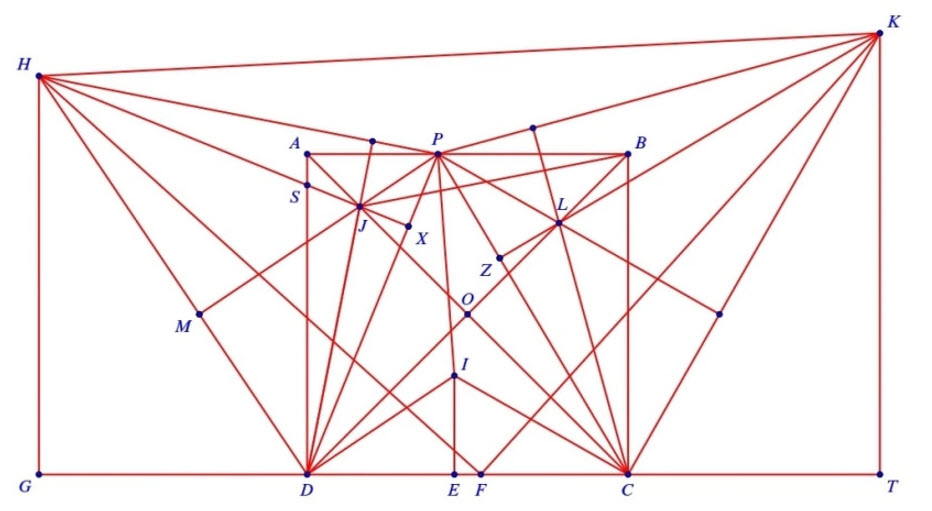
a) Hai tam giác \(A J D\) và \(A J B\) bằng nhau ( \(\mathrm{c}-\mathrm{g}-\mathrm{c}\) ) nên \(\angle A D J=\angle A B J=\angle P D J\). Từ đó suy ra tứ giác \(B D J P\) nội tiếp.
b) Gọi \(M\) là giao điểm của hai đường thẳng \(P J\) và \(H D\). Vì \(\angle D B P=45^{\circ}\) nên \(\angle M J D=45^{\circ}\), suy ra \(\angle M D J=45^{\circ}\). Từ đây, ta có \(\angle D H P=45^{\circ}\). Mặt khác, ta lại có \(\angle J H P=\angle J D P=\angle J D S\) nên \(\angle D H P-\angle S H P=\angle M D J-\angle J D S\). Từ đó \(\angle S H D=\angle S D H\), suy ra \(S H=S D\).
c) Gọi \(Z\) là giao điểm của đường thẳng \(K L\) và đường thẳng \(P C ; X\) là giao điểm của đường thẳng \(H J\) và \(P D\). Gọi \(G, T\) tương ứng là hình chiếu vuông góc của các điểm \(H, K\) trên đường thẳng \(C D\). Ta có \(\angle D H G=\angle S D H=\angle S H D\), do đó
\[ D G=D X=\dfrac{D A+D P-A P}{2} \]
Hoàn toàn tương tự, ta cũng có \(C T=C Z=\dfrac{C P+C B-B P}{2}\) và \(C F=D E=\dfrac{D C+D P-C P}{2}\). Đến đây, với chú ý tam giác \(H P D\) có \(\angle P H D=45^{\circ}\) và \(J\) là trực tâm tam giác, ta dễ dàng chứng minh được \(H J=D P\) (đây là một kết quả quen thuộc). Lại có \(J X=\dfrac{A P+A D-D P}{2}\) nên
\[ H X=\dfrac{A D+A P+D P}{2}=C F+C T=T F \]
Chứng minh tương tự, ta có \(K T=F G\). Từ đó \(\triangle G H F=\triangle T F K\) ( \(\mathrm{c}-\mathrm{g}-\mathrm{c}\) ). Từ đây, ta dễ dàng suy ra tam giác \(F H K\) vuông cân.
Bài 4
(1 điểm)
Cho bảng ô vuông kích thước ( \(2023 \times 2023\) ), ô vuông có kích thước \((1 \times 1)\) được gọi là ô vuông đơn vị. Mỗi ô vuông đơn vị của bảng được tô bằng một trong 2 màu đen hoặc trắng sao cho mỗi ô vuông đơn vị tô màu đen được kề với ít nhất 3 ô vuông đơn vị tô màu trắng ( 2 ô vuông đơn vị có cạnh chung được gọi là kề nhau). Hỏi số ô vuông đơn vị được tô màu đen nhiều nhất là bao nhiêu?
Cách giải 1:
Bảng ô vuông đã cho có thể chia thành 1022121 bảng con kích thước \(2 \times 2,1011\) bảng con kích thước \(2 \times 1\) ở rìa phải của bảng đã cho, 1011 bảng con kích thước \(1 \times 2\) ở rìa bên dưới của bảng đã cho và một bảng con kích thước \(1 \times 1\) ở góc dưới bên phải. Ta thấy
- Mỗi bảng con \(2 \times 2\) có nhiều nhất hai ô vuông được tô màu đen. (Nếu có ba ô vuông được tô màu đen thì sẽ có một ô đen mà chỉ có không quá hai ô kề với nó được tô màu trắng, mâu thuẫn.)
- Mỗi bảng con \(2 \times 1\) có nhiều nhất một ô vuông được tô màu đen. (Nếu cả hai ô vuông đều được tô màu đen thì mỗi ô sẽ có không quá hai ô kề với nó được tô màu trắng, mâu thuẫn.)
- Mỗi bảng con \(1 \times 2\) có nhiều nhất một ô vuông được tô màu đen. (Nếu cả hai ô vuông đều được tô màu đen thì mỗi ô sẽ có không quá hai ô kề với nó được tô màu trắng, mâu thuẫn.)
- Bảng con \(1 \times 1\) ở góc dưới bên phải chỉ có hai ô kề với nó nên được tô màu trắng.
Như vậy, số ô vuông được tô màu đen không vượt quá \(1022121 \cdot 2+1011+1011=2046264\). Mặt khác, cách tô màu sau thỏa mãn yêu cầu bài toán.

Vậy, số ô vuông được tô màu đen nhiều nhất là 2046264.