Bài 1
(3.5 điểm)
a) Giải hệ phương trình
\[ \left\{\begin{array}{l} x^4+4 y^2-5 x^2 y^2=4 \\ (3 x+4 y-2)\left(x^2+2 y^2-3 x y\right)=4 \end{array}\right. \]
b) Giải phương trình
\[ \sqrt{x}+\sqrt{3-2 x}=1+\sqrt{2-x}+\frac{1}{3} \sqrt{x-1} \]
Cách giải 1:
a) Phương trình thứ nhất của hệ có thể được viết lại thành
\[ (x+y)(x+2 y)\left(x^2+2 y^2-3 x y\right)=4 \]
Kết hợp với phương trình thứ hai của hệ, ta được
\[ (x+y)(x+2 y)=3 x+4 y-2=2(x+y)+(x+2 y)-2 \]
Từ đó \((x+2 y-2)(x+y-1)=0\). Xét các trường hợp, ta tìm được tất cả các nghiệm \((x, y)\) của hệ phương trình là \((0,1),\left(\dfrac{\sqrt{97}-1}{6}, \dfrac{13-\sqrt{97}}{12}\right),\left(\dfrac{-\sqrt{97}-1}{6}, \dfrac{13+\sqrt{97}}{12}\right)\).
b) Điều kiện: \(1 \leq x \leq \dfrac{3}{2}\). Phương trình đã cho tương đương với
\[ (\sqrt{x}-1)+(\sqrt{3-2 x}-\sqrt{2-x})=\dfrac{1}{3} \sqrt{x-1} \]
hay
\[ \dfrac{x-1}{\sqrt{x}+1}-\dfrac{x-1}{\sqrt{3-2 x}+\sqrt{2-x}}=\dfrac{1}{3} \sqrt{x-1} \]
Hiển nhiên \(x=1\) là nghiệm của phương trình. Xét trường hợp \(1
\[ \dfrac{1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{3-2 x}+\sqrt{2-x}}=\dfrac{1}{3 \sqrt{x-1}} \]
Vì \(1\sqrt{3-2 x}\) và \(1>\sqrt{2-x}\), suy ra \(\sqrt{x}+1>\sqrt{3-2 x}+\sqrt{2-x}\). Như vậy \(\mathrm{VT}_{(1)}<0<\mathrm{VP}_{(1)}\). Ta suy ra phương trình (1) vô nghiệm. Vậy, phương trình đã cho có nghiệm duy nhất \(x=1\).
Bình luận. Ngoài cách làm trên, ta cũng có cách làm khác cho ý b) như sau: Với điều kiện xác định \(1 \leq x \leq \dfrac{3}{2}\), ta có
\[ \begin{aligned} \sqrt{x}+\sqrt{3-2 x} & =\sqrt{3-x+2 \sqrt{3 x-2 x^2}}=\sqrt{3-x+2 \sqrt{2-x-2(x-1)^2}} \\ & \leq \sqrt{3-x+2 \sqrt{2-x}}=1+\sqrt{2-x} \end{aligned} \]
Vì thế \(\sqrt{x}+\sqrt{3-2 x} \leq 1+\sqrt{2-x} \leq 1+\sqrt{2-x}+\dfrac{1}{3} \sqrt{x-1}\). Tuy nhiên, theo đề bài thì dấu đẳng thức phải xảy ra, tức ta phải có \(x=1\).
Bài 2
(2.5 điểm)
a) Tất cả các số nguyên dương \(x, y\) thỏa mãn
\[ (x+y)^3+6 x y+3 y^2+y=8 x^3+9 x^2+1 \]
b) Xét các số thực dương \(x_1, x_2, \ldots, x_{2024}\) thỏa mãn \(x_1 x_2 \cdots x_{2024}=1\). Tìm giá trị nhỏ nhất của biểu thức
\[ P=\left(x_1^2-x_1+1\right)\left(x_2^2-x_2+1\right) \cdots\left(x_{2024}^2-x_{2024}+1\right) \]
Cách giải 1:
a) Phương trình đã cho có thể được viết lại thành
\[ (x+y)^3+3(x+y)^2+6 x+y=(2 x+1)^3 \]
Suy ra \((x+y)^3+3(x+y)^2+6 x+y\) là số lập phương. Mà
\[ (x+y)^3<(x+y)^3+3(x+y)^2+6 x+y<(x+y)^3+6(x+y)^2+12(x+y)+8=(x+y+2)^3 \]
nên \((x+y)^3+3(x+y)^2+6 x+y=(x+y+1)^3\), hay \(3 x=2 y+1\).
Ngoài ra, từ kết quả trên, ta cũng có \((x+y+1)^3=(2 x+1)^3\) nên \(x+y+1=2 x+1\).
Từ đây, ta dễ dàng suy ra \(x=y=1\). Thử lại, ta thấy thỏa mãn. Vậy, có duy nhất một cặp số nguyên dương \((x, y)\) thỏa mãn yêu cầu đề bài là \((1,1)\).
b) Với mỗi số thực dương \(x\), ta có \(x^2-x+1=(x-1)^2+x \geq x\). Sử dụng bất đẳng thức này, ta có \(P \geq x_1 x_2 x_3 \cdots x_{2024}=1\). Mặt khác, với \(x_1=x_2=\cdots=x_{2024}=1\) thì \(P=1\). Vậy \(\min P=1\).
Bình luận. Ngoài cách làm trên, ý a) của bài toán còn có cách làm khác như sau: Phương trình có thể được viết lại thành \((x+y)^3-8 x^3+\left(3 y^2+6 x y-9 x^2\right)=-(y-1)\), hay
\[ (y-x)\left[(x+y)^2+2 x(x+y)+4 x^2+3(y+2 x)\right]=-(y-1) \]
Từ đây, ta suy ra \(y-1\) chia hết cho \((x+y)^2+2 x(x+y)+4 x^2+3(y+2 x)\). Tuy nhiên, vì \(0 \leq y-1<y<(x+y)^2+2 x(x+y)+4 x^2+3(y+2 x)\) nên điều này xảy ra chỉ khi \(y=1\). Thay trở lại phương trình, ta được \(x=y=1\).
Bài 3
(3 điểm)
Cho tam giác \(A B C\) nhọn, không cân nội tiếp đường tròn \((O)\), có \(E, F\) lần lượt là trung điểm của các cạnh \(C A, A B\). Điểm \(P\) di chuyển trên cung nhỏ \(B C(P\) khác \(B, C)\). Gọi \(M, N\) lần lượt là giao điểm của các đường thẳng \(P C, P B\) với đường thẳng \(E F\). Các đường thẳng \(A M, A N\) cắt đường tròn \((O)\) theo thứ tự tại \(Q, R(Q, R\) khác \(A)\).
a) Chứng minh rằng tứ giác \(A F P M\) nội tiếp và \(\angle E P F=\angle Q P R\).
b) Chứng minh rằng giao điểm của hai đường thẳng \(Q E\) và \(R F\) nằm trên đường tròn \((O)\).
c) Lấy các điểm \(S, T\) lần lượt thuộc các đường thẳng \(C A, A B\) sao cho ba đường thẳng \(E T, F S, A P\) song song với nhau. Gọi \(K\) và \(L\) lần lượt là tâm đường tròn ngoại tiếp của các tam giác \(N F S\) và \(M E T\). Đường thẳng qua điểm \(K\) vuông góc với đường thẳng \(A B\) cắt đường thẳng qua điểm \(L\) vuông góc với đường thẳng \(A C\) tại điểm \(J\). Chứng minh rằng điểm \(J\) luôn nằm trên một đường thẳng cố định khi điểm \(P\) thay đổi.
Cách giải 1:
a) Ta có \(E F \| B C\) nên \(\angle P M F=\angle P C B=\angle P A B\), suy ra tứ giác \(A F P M\) nội tiếp. Chứng minh tương tự, ta cũng có tứ giác \(A E P N\) nội tiếp. Từ đây, ta có
\[ \angle E P F=\angle A P F+\angle A P E=\angle A M F+\angle A N E=180^{\circ}-\angle M A N=\angle Q P R \]
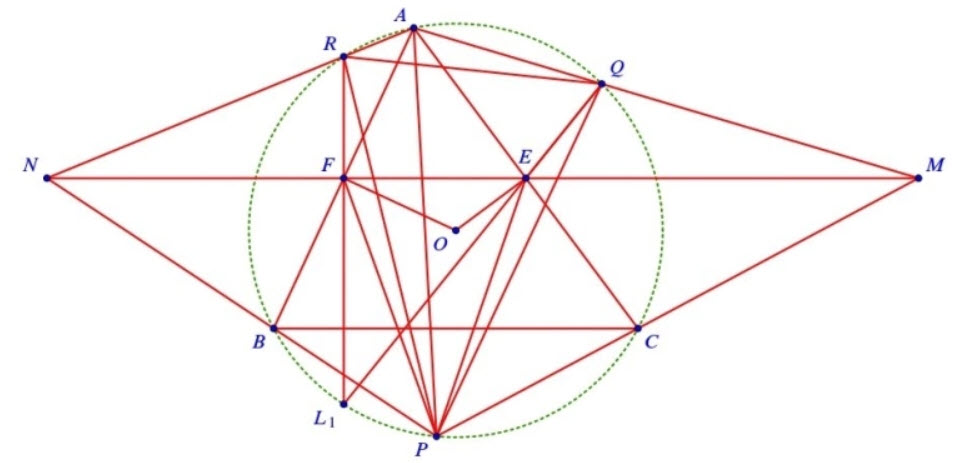
b) Ta có \(\angle P F M=\angle P A M=\angle P R Q\), mà \(\angle E P F=\angle R P Q\), nên hai tam giác \(P F E\) và \(P R Q\) đồng dạng \((\mathrm{g}-\mathrm{g})\). Từ đây, ta dễ dàng suy ra hai tam giác \(P F R\) và \(P E Q\) đồng dạng (c-g-c). Từ đó \(\angle P R F=\angle P Q E\).
Bây giờ, gọi \(L_1\) là giao điểm của hai đường thẳng \(Q E\) và \(R F\). Thế thì tứ giác \(P L_1 R Q\) là tứ giác nội tiếp, từ đó suy ra điểm \(L_1\) thuộc đường tròn \((O)\).
c) Ta có bổ đề sau.
Bổ đề. Cho tứ giác \(A B C D\) nội tiếp đường tròn \((O)\), các đường chéo \(A C\) và \(B D\) cắt nhau tại điểm I. Gọi \(H\) là hình chiếu vuông góc của điểm I trên đuoờng thẳng \(C D\) và \(M\) là trung điểm của đoạn thẳng \(C D\). Các điểm \(N, P\) lần lượt thuộc các đuờng thẳng \(B C, A D\) sao cho \(M N \| A C\) và \(M P \| B D\). Đường tròn ngoại tiếp tam giác \(M N P\) cắt đường thẳng \(C D\) lần thứ hai tại điểm \(K\). Khi đó, \(M\) là trung điểm của đoạn thẳng \(H K\).
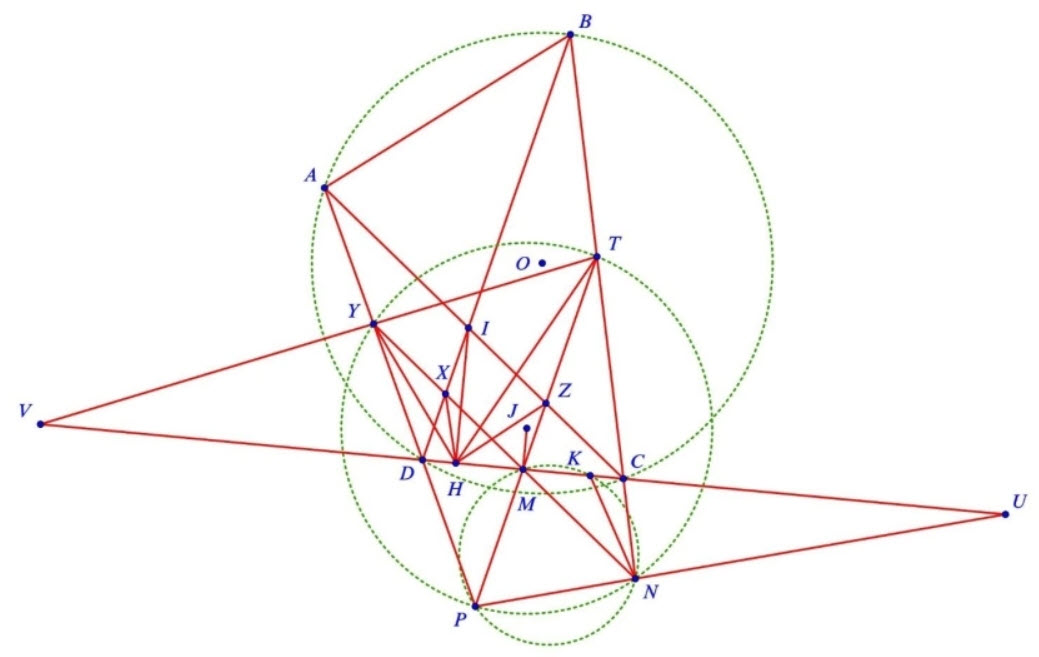
Chứng minh. Gọi \(X, Y\) lần lượt là giao điểm của đường thẳng \(M N\) và các đường thẳng \(D I\), \(D A ; Z, T\) lần lượt là giao điểm của đường thẳng \(M P\) và các đường thẳng \(C I, C B\). Ta thấy \(X\), \(Y, Z, T\) lần lượt là trung điểm của các đoạn thẳng \(D I, D A, C I, C B\) và tứ giác \(M H X Z\) là hình thang cân.
Từ \(\angle H X Y=\angle H Z T\) và \(\dfrac{X H}{X Y}=\dfrac{I D}{I A}=\dfrac{I C}{I B}=\dfrac{Z H}{Z T}\), ta suy ra \(\triangle H X Y \sim \triangle H Z T\) (c-g-c). Từ đó \(\angle H Y X=\angle H T Z\). Suy ra, tứ giác \(H M T Y\) nội tiếp.
Chú ý rằng \(N Y \| A C\) và \(P T \| B D\), ta có \(\angle N Y P=\angle D A C=\angle D B C=\angle N T P\). Suy ra, tứ giác \(N P Y T\) nội tiếp.
Gọi \((J)\) là đường tròn ngoại tiếp tứ giác \(N P Y T\). Do \(M\) là trung điểm của đoạn thẳng \(C D\) nên theo định lý con bướm đảo, ta có \(J M \perp C D\). Gọi \(U, V\) lần lượt là giao điểm của đường thẳng \(C D\) và các đường thẳng \(N P Y T\). Áp dụng định lý con bướm thuận, ta có \(M\) là trung điểm của đoạn thẳng \(U V\).
Vì \(\angle N Y T=\angle N P T=\angle U K N\) nên tứ giác \(N K Y V\) nội tiếp. Chứng minh tương tự, tứ giác \(N H Y U\) nội tiếp. Suy ra \(M H \cdot M U=M N \cdot M Y=M K \cdot M V\). Lại có \(M U=M V\) nên \(M H=M K\). Vậy, \(M\) là trung điểm của đoạn thẳng \(H K\). Bổ đề được chứng minh.
Trở lại bài toán, ta xét trường hợp các điểm ở vị trí như trong hình vẽ (xem trang sau), các trường hợp còn lại chứng minh tương tự.
Gọi \(X\) là giao điểm khác \(F\) của đường tròn \((K)\) và đường thẳng \(A B\). Qua điểm \(D\), kẻ đường thẳng vuông góc với đường thẳng \(A B\) tại điểm \(Y\). Gọi \(Z, G\) lần lượt là giao điểm của đường thẳng \(K J\) và các đường thẳng \(A B, E F\). Gọi \(H\) là giao điểm của hai đường thẳng \(L J\) và \(E F\) tại \(H\). Gọi \(U, V\) lần lượt là giao điểm của đường thẳng \(B C\) và các đường thẳng \(O E, O F\).
Áp dụng bổ đề trên, ta có \(F\) là trung điểm của đoạn thẳng \(X Y\).
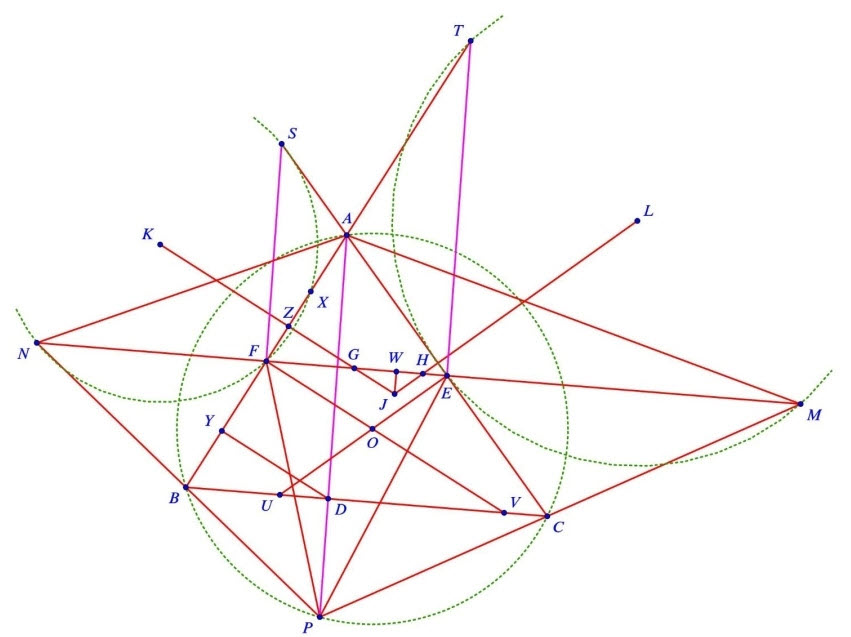
Do \(\dfrac{F G}{F Z}=\dfrac{B D}{B Y}=\dfrac{D V}{F Y}\) và \(F Y=F X=2 F Z\) nên \(F G=\dfrac{D V}{2}\). Lập luận tương tự, ta cũng có \(E H=\dfrac{D U}{2}\). Do đó \(F G+H E=\dfrac{U V}{2}\). Suy ra \(G H=E F-(F G+E H)=\dfrac{B C-U V}{2}\) không đổi. Tam giác \(J G H\) có các góc khồng đổi và cạnh \(G H\) có độ dài không đổi nên đường cao \(J W\) của tam giác có độ dài bằng \(h\) không đổi. Vậy, điểm \(J\) thuộc đường thẳng song song \(E F\) cách \(E F\) một khoảng bằng \(h\) cố định.
Bài 4
(1 điểm)
Tìm tất cả các số nguyên dương \(m\) sao cho có thể cắt hình vuông có cạnh bằng \(m\) thành đúng 5 hình chữ nhật mà độ dài 10 cạnh của 5 hình chữ nhật đó được lấy từ các số \(1,2,3,4,5,6,7,8,9,10\) và mỗi số được lấy đúng một lần.
Cách giải 1:
Gọi \(a_1, b_1\) lần lượt là chiều dài và chiều rộng của hình chữ nhật thứ nhất; \(a_2, b_2\) lần lượt là chiều dài và chiều rộng của hình chữ nhật thứ hai; \(\ldots ; a_5, b_5\) lần lượt là chiều dài và chiều rộng của hình chữ nhật thứ năm. Khi đó, ta có diện tích của vuông đã cho bằng
\[ m^2=a_1 b_1+a_2 b_2+a_3 b_3+a_4 b_4+a_5 b_5 \]
Sử dụng bất đẳng thức AM-GM, ta có
\[ m^2 \geq 5 \sqrt[5]{a_1 a_2 a_3 a_4 a_5 b_1 b_2 b_3 b_4 b_5}=5 \sqrt[5]{10!}>100 \]
và
\[ m^2 \leq \dfrac{a_1^2+b_1^2}{2}+\dfrac{a_2^2+b_2^2}{2}+\dfrac{a_3^2+b_3^2}{2}+\dfrac{a_4^2+b_4^2}{2}+\dfrac{a_5^2+b_5^2}{2}=\dfrac{1^2+2^2+\cdots+10^2}{2}=\dfrac{385}{2} \]
Như vậy \(100
- Với \(m=11\), cách chia hình sau thỏa mãn yêu cầu đề bài.
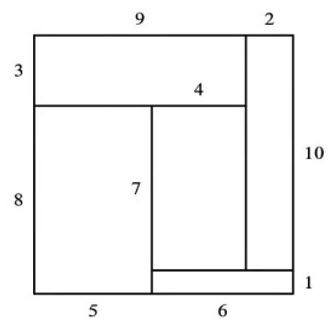
- Với \(m=13\), cách chia hình sau thỏa mãn yêu cầu đề bài.
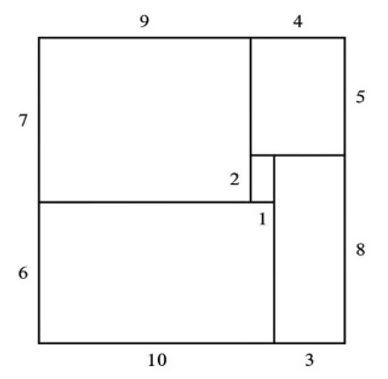
- Nếu \(m=12\) thỏa mãn thì cách chia thỏa mãn yêu cầu đề bài phải chia theo phương song song với các cạnh của hình vuông đã cho và sẽ có bốn hình chữ nhật mà hai trong các cạnh của mỗi hình chữ nhật thu được nằm trên hình vuông lớn.
Nếu một hình chữ nhật nào đó trong bốn hình chữ nhật nói trên có cạnh bằng 6 , thì sẽ có hình chữ nhật "kề" với nó cũng có cạnh bằng 6 , vô lý. Như vậy, trong bốn hình chữ nhật nằm ở "rìa" cạnh hình vuông không có hình chữ nhật nào có cạnh bằng 6 .
Nếu trong bốn hình chữ nhật nằm ở "rìa" cạnh hình vuông có hình chữ nhật có cạnh bằng 1 , thì sẽ có hình chữ nhật "kề" với nó có cạnh bằng 11, vô lý. Như vậy, trong bốn hình chữ nhật nằm ở "rìa" cạnh hình vuông không có hình chữ nhật nào có cạnh bằng 1 .
Suy ra, hình chữ nhật ở phía trong hình vuông phải có một cạnh bằng 1 và một cạnh bằng 6. Và vì thế, phải có hai hình chữ nhật kề nhau ở "rì"" cạnh hình vuông có độ dài cạnh hơn kém nhau 1 đơn vị.
Ta thấy các cạnh của các hình chữ nhật kề nhau nằm ở "rìa" cạnh hình vuông phải lần lượt là 2,\(10 ; 3,9 ; 4,8 ; 5,7\). Ta thấy không có cặp số nào có khoảng cách bằng 1 nên không thể chia được hình như yêu cầu, mâu thuẫn.
Vậy \(m=11\) và \(m=13\) là các số cần tìm.