Bài 1
(7 điểm)
Xét đa thức \(P(x)=x^4-x^3+x\).
a) Chứng minh rằng với mọi số dương \(a\), đa thức \(P(x)-a\) có duy nhất một nghiệm dương.
b) Xét dãy số \(\left(a_n\right)\) được xác định bởi \(a_1=\dfrac{1}{3}\) và với mọi \(n \geq 1, a_{n+1}\) là nghiệm dương của đa thức \(P(x)-a_n\). Chứng minh rằng dãy \(\left(a_n\right)\) có giới hạn hữu hạn và tìm giới hạn đó.
Cách giải 1:
a) Xét hàm số \(f(x)=P(x)-a\) trên miền \([0,+\infty)\), ta có
\[f^{\prime}(x)=4 x^3-3 x^2+1=2 x^3+(2 x+1)(x-1)^2>0\]
với mọi \(x>0\). Do đó, hàm số \(f\) tăng ngặt trên miền \([0, \infty)\). Mặt khác, ta lại có \(f(0)=-a<0\) và \(\lim _{x \rightarrow+\infty} f(x)=+\infty\) nên phương trình \(f(x)=0\) có nghiệm thực dương duy nhất. Từ đây, ta có điều phải chứng minh.
b) Theo câu a), dễ thấy \(a_n\) được xác định một cách duy nhất. Ta có \(a_{n+1}^4-a_{n+1}^3+a_{n+1}=a_n\), do đó
\[a_n-1=\left(a_{n+1}-1\right)\left(a_{n+1}^3+1\right), \quad \forall n \geq 1\]
Vi \(a_1<1\) nên từ đây, bằng quy nạp, ta chứng minh được \(a_n<1\) với mọi \(n\) nguyên dương. Và vì thế, ta cũng có \(a_n-a_{n+1}=a_{n+1}^3\left(a_{n+1}-1\right)<0\), suy ra dãy \(\left(a_n\right)\) tăng ngặt. Như vậy, dãy \(\left(a_n\right)\) tăng ngặt và bị chặn trên bởi 1 nên tồn tại giới hạn \(\lim a_n=L\) với \(0<L<1\).
Bây giờ, chuyển phương trình (1) sang giới hạn, ta được \(L-1=(L-1)\left(L^3+1\right)\), hay \(L^3(L-1)=0\). Từ đó \(L=1\). Vậy \(\lim a_n=1\).
Bình luận. Ngoài cách làm trên, chúng ta cũng có thể sử dụng nguyên lý ánh xạ co. Cụ thể, với chú ý hàm số \(g(x)=x^4-x^3+x\) tăng ngặt trên miền \([0,+\infty)\) và \(f\left(\dfrac{1}{3}\right)<\dfrac{1}{3}=a_1\), ta thấy ngay \(a_2>\dfrac{1}{3}\) và từ đó, bằng quy nạp, ta sẽ chứng minh được \(a_n>\dfrac{1}{3}\) với mọi số nguyên dương \(n\). Lúc này, ta có ngay
\[\left|1-a_{n+1}\right|=\dfrac{1}{a_{n+1}^3+1}\left|1-a_n\right| \leq \dfrac{1}{\dfrac{1}{27}+1}\left|1-a_n\right|=\dfrac{27}{28}\left|1-a_n\right|, \quad \forall n \geq 1\]
Từ đây, dễ thấy ngay \(\lim a_n=1\).
Bài 2
(7 điểm)
Với mỗi số nguyên \(n \geq 0\), đặt \(u_n=(2+\sqrt{5})^n+(2-\sqrt{5})^n\).
a) Chứng minh rằng \(u_n\) là số nguyên dương với mọi \(n \geq 0\). Khi \(n\) thay đổi, số dư của \(u_n\) khi chia cho 24 lớn nhất bằng bao nhiêu?
b) Tìm tất cả các cặp số nguyên dương \((a, b)\) với \(a, b\) nhỏ hơn 500 sao cho với mọi \(n\) lẻ ta có \(u_n \equiv a^n-b^n(\bmod 1111)\).
Cách giải 1:
a) Từ giả thiết, ta dễ dàng chứng minh được \(u_{n+2}=4 u_{n+1}+u_n\) với mọi số tự nhiên \(n\). Đến đây, bằng tính toán trực tiếp, ta dễ thấy dãy số dư khi chia các số hạng của dãy \(\left(u_n\right)\) cho 24 tuần hoàn theo chu kỳ \(8: 2,4,18,4,10,20,18,20\). Như vậy, khi \(n\) thay đổi, số dư của \(u_n\) khi chia cho 24 lớn nhất là 20 .
b) Xét một cặp số \((a, b)\) thỏa mãn yêu cầu đề bài. Cho \(n=1\) và \(n=3\), ta được \(a-b \equiv 4(\bmod 1111)\) và \(a^3-b^3 \equiv 76(\bmod 1111)\). Từ đó
\[76 \equiv(a-b)^3+3 a b(a-b) \equiv 64+12 a b \quad(\bmod 1111)\]
Suy ra \(a b \equiv 1(\bmod 1111)\), hay \(b(b+4) \equiv 1(\bmod 1111)\). Một cách tương đương, ta có
\[(b+2)^2 \equiv 5 \quad(\bmod 1111)\]
Từ đó \((b+2)^2 \equiv 5(\bmod 11)\) và \((b+2)^2 \equiv 5(\bmod 101)\).
Vì \((b+2)^2 \equiv 5 \equiv 16(\bmod 11)\) nên \(b \equiv 2,5(\bmod 11)\).
Vì \((b+2)^2 \equiv 5 \equiv 45^2(\bmod 101)\) nên \(b \equiv 43,54(\bmod 101)\).
Kết hợp hai kết quả lại, ta suy ra \(b\) phải có một trong các dạng \(1111 k+750,1111 k+761,1111 k+346\) hoặc \(1111 k+357\) với \(k\) nguyên. Mà \(1 \leq b<500\) nên \(b \in\{346,357\}\). Kết hợp với \(a \equiv b(\bmod 1111)\) và \(1 \leq a<500\), ta được \((a, b) \in\{(350,346),(361,357)\}\).
Bây giờ, ta sẽ chứng minh hai cặp số \((350,346)\) và \((361,357)\) thỏa mãn yêu cầu đề bài. Dễ thấy với hai cặp số \((a, b)\) như trên, ta có \(a^2 \equiv 4 a+1(\bmod 1111)\) và \(b^2 \equiv-4 b+1(\bmod 1111)\). (Ta có thể suy ra điều này từ \(a-b \equiv 4(\bmod 1111)\) và \(a b \equiv 1(\bmod 1111)\) mà không phải tính toán gì.)
Bằng quy nạp, ta sẽ chứng minh với mọi số tự nhiên \(m\), thì \(u_{2 m+1} \equiv a^{2 m+1}-b^{2 m+1}(\bmod 1111)\) với mọi số nguyên dương \(n\) lẻ và \(u_{2 m} \equiv a^{2 m}+b^{2 m}(\bmod 1111)\). Với \(m=0\) và \(m=1\), khẳng định hiển nhiên đúng. Giả sử khẳng định đúng đến \(m\) với \(m\) nguyên dương. Sử dụng giả thiết quy nạp, ta có
\[\begin{aligned}u_{2 m+2} & =4 u_{2 m+1}+u_{2 m} \equiv 4\left(a^{2 m+1}-b^{2 m+1}\right)+a^{2 m}+b^{2 m} \\& \equiv(4 a+1) a^{2 m}+(1-4 b) b^{2 m} \equiv a^{2 m+2}+b^{2 m+2} \quad(\bmod 1111)\end{aligned}\]
Từ đó
\[\begin{aligned}u_{2 m+3} & =4 u_{2 m+2}+u_{2 m+1} \equiv 4\left(a^{2 m+2}+b^{2 m+2}\right)+a^{2 m+1}-b^{2 m+1} \\& \equiv(4 a+1) a^{2 m+1}+(4 b-1) b^{2 m+1} \equiv a^{2 m+3}-b^{2 m+3} \quad(\bmod 1111)\end{aligned}\]
Như vậy, khẳng định cũng đúng với \(m+1\). Theo nguyên lý quy nạp, ta có khẳng định đúng với mọi số tự nhiên \(m\).
Vậy, có hai cặp số thỏa mãn yêu cầu đề bài là \((350,346)\) và \((361,357)\).
Bài 3
(6 điểm)
Cho tam giác nhọn không cân \(A B C\) nội tiếp đường tròn \((O)\) và có trực tâm \(H\). Đường thẳng \(A H\) cắt lại \((O)\) tại điểm \(D\) khác \(A\). Gọi \(E\) và \(F\) tương ứng là trung điểm các đoạn thẳng \(A B\) và \(A C\). Đường thẳng đi qua \(H\) và vuông góc với \(H F\) cắt đường thẳng \(B C\) tại điểm \(K\).
a) Đường thẳng \(D K\) cắt lại \((O)\) tại điểm \(Y\) khác \(D\). Chứng minh rằng giao điểm của đường thẳng \(B Y\) và đường trung trực của đoạn thẳng \(B K\) nằm trên đường tròn ngoại tiếp tam giác \(O F Y\).
b) Đường thẳng đi qua \(H\) và vuông góc với \(H E\) cắt đường thẳng \(B C\) tại điểm \(L\). Đường thẳng \(D L\) cắt lại \((O)\) tại điểm \(Z\) khác \(D\). Gọi \(M, N\) và \(P\) tương ứng là giao điểm của các cặp đường thẳng \((B Z, O E),(C Y, O F)\) và \((B Y, C Z)\). Gọi \(T\) là giao điểm của cặp đường thẳng \((Y Z, M N)\) và \(d\) là đường thẳng đi qua \(T\) và vuông góc với \(O A\). Chứng minh rằng \(d\) đi qua trung điểm của đoạn thẳng \(A P\).
Cách giải 1:
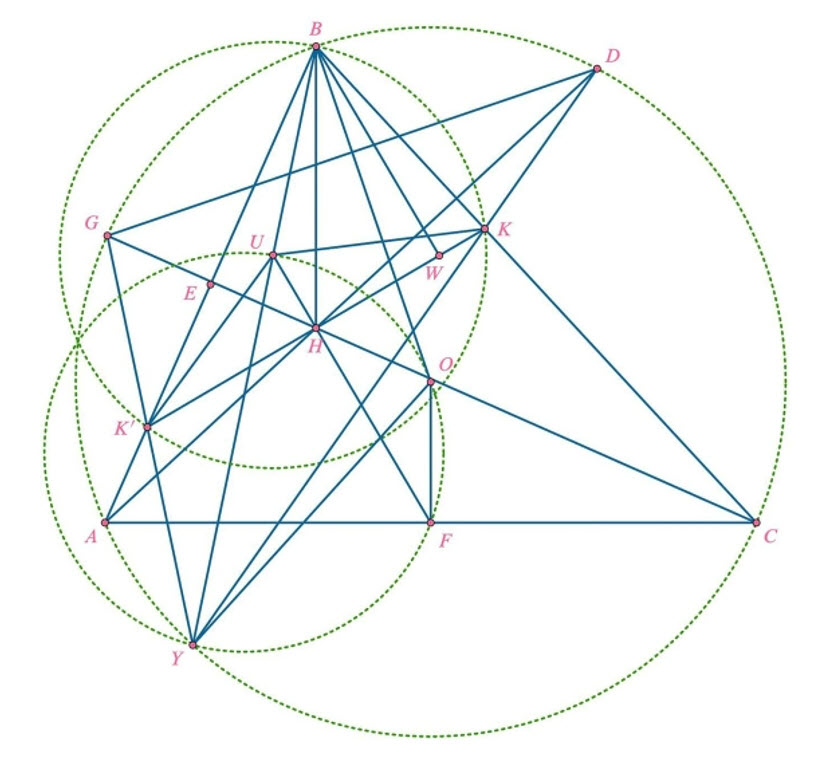
a) Gọi \(K^{\prime}\) là giao điểm của hai đường thẳng \(H K\) và \(B A\). Do \(K K^{\prime} \perp H F\) nên ta có kết quả quen thuộc \(H K=H K^{\prime}\). Gọi \(G\) là giao điểm thứ hai của đường thẳng \(C H\) và đường tròn \((O)\), ta có \(\angle B G K^{\prime}+\angle B D K=\angle B H K^{\prime}+\angle B H K=180^{\circ}\). Do đó, ba điểm \(G, K^{\prime}, Y\) thẳng hàng.
Do \(B G=B H=B D\) nên \(Y B\) là tia phân giác của góc \(G Y D\).
Gọi \(U\) là tâm của đường tròn \(\left(B K K^{\prime}\right)\). Do \(U\) thuộc đường trung trực của đoạn thẳng \(K K^{\prime}\) nên ba điểm \(U, H, F\) thẳng hàng. Từ đây, ta có \(\angle K^{\prime} U K=2 \angle K^{\prime} B K=\angle G B D\), do đó tứ giác \(U K^{\prime} Y K\) nội tiếp. Mà \(U K=U K^{\prime}\) nên \(Y U\) là tia phân giác của góc \(K^{\prime} Y K\). Suy ra ba điểm \(Y, U, B\) thẳng hàng.
Qua điểm \(B\), kẻ đường thẳng \(B W\) vuông góc với đường thẳng \(K K^{\prime}\) tại điểm \(W\). Ta có hai tia \(B U, B W\) đẳng giác trong góc \(A B C\) Và hai tia \(B H, B O\) đẳng giác trong góc \(A B C\) nên \(\angle U B O=\angle H B W\). Lại có \(\angle U B O=\angle U Y O\) và \(\angle H B W=\angle O F H\) (Vì \(F H \| B W\) và \(F O \| B H\) ). Do đó \(\angle O Y U=\angle O F U\) nên tứ giác \(O F Y U\) nội tiếp. Vì \(U B=U K\) nên đường thẳng \(B Y\) cắt đường trung trực của đoạn thẳng \(B K\) tại điểm \(U\) thuộc đường tròn \((O F Y)\).
b) Kẻ các đường kính \(B B^{\prime}\) và \(C C^{\prime}\) của đường tròn \((O)\). Ta có tứ giác \(A H C B^{\prime}\) là hình bình hành nên \(F\) là trung điểm của đoạn thẳng \(H B^{\prime}\).
Vi \(\angle C M F=90^{\circ}-\angle A C Y=90^{\circ}-\angle U B K^{\prime}=\angle B K K^{\prime}=\angle F H A=\angle F B^{\prime} C\) nên tứ giác \(C F M B^{\prime}\) nội tiếp. Từ đó \(\angle C B^{\prime} M=90^{\circ}\), suy ra điểm \(M\) thuộc đường thẳng \(B^{\prime} C^{\prime}\). Chứng minh tương tự, ta cũng có điểm \(N\) thuộc đường thẳng \(B^{\prime} C^{\prime}\).
Ta có tứ giác \(B Z Y C\) nội tiếp, mà \(M N \| B C\), nên theo định lý Riem, tứ giác \(Y Z N M\) nội tiếp.
Ví \(\angle A N Z=2 \angle A B Z=\angle A O Z\) nên tứ giác \(A O N Z\) nội tiếp. Tương tự, ta có tứ giác \(A O M Y\) nội tiếp, mà tứ giác \(Z N M Y\) nội tiếp nên các đường thẳng \(Z N, Y M, A O\) dồng quy tại điểm \(S\).
Gọi \(R\) là giao điểm của hai đường thẳng \(O N\) và \(A Z ; X\) là giao điểm của hai đường thẳng \(O F\) và \(A Y\). Áp dụng định lý Desargues cho hai tam giác \(A Y Z\) và \(O M N\) có ba đường thẳng \(A O, Y M, Z N\) đồng quy tại điểm \(S\), ta suy ra ba điểm \(T, R, X\) thẳng hàng.
Do tứ giác \(A O N Z\) nội tiếp và \(O A=O Z\) nên \(O N \cdot O R=O A^2=R^2\). Tương tự, \(O M \cdot O X=R^2\). Kẻ đường thẳng \(X J\) vuông góc với đường thẳng \(O A\) tại điểm \(J\). Ta có \(O J \cdot O A=O F \cdot O X=O E \cdot O R\) nên hai đường thẳng \(R J\) và \(O A\) vuông góc với nhau.
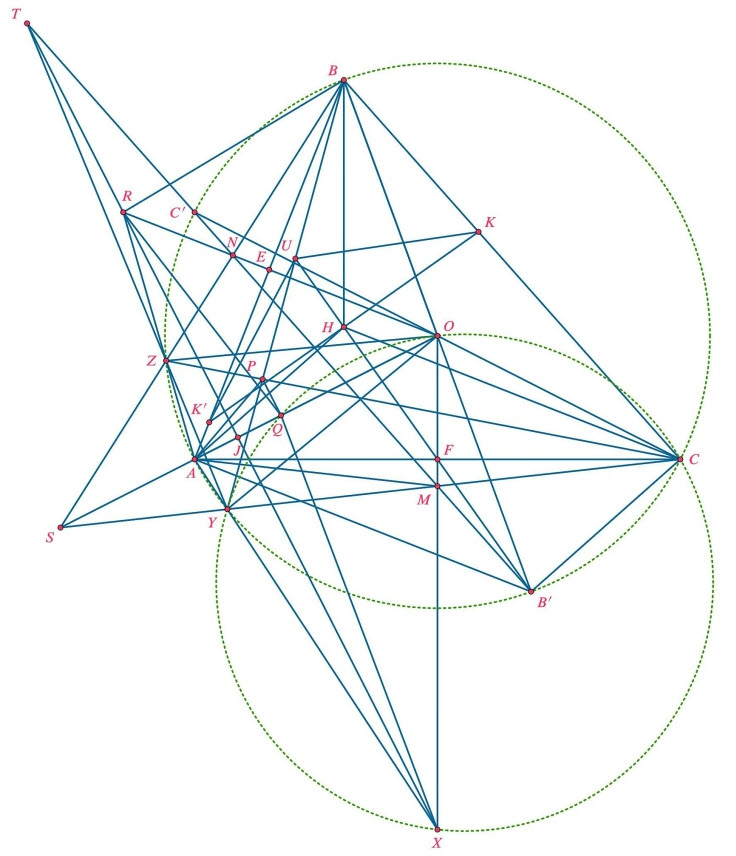
Gọi \(Q\) là điểm đối xứng với điểm \(A\) qua điểm \(J\). Khi đó, dễ thấy điểm \(Q\) thuộc đường thẳng \(O A\) và \(\angle R Q A=\angle R A Q=\angle R B O\), do đó tứ giác \(O Q R B\) nội tiếp.
Ta cũng có \(\angle O Z A=\angle O A Z=\angle O B R\) nên tứ giác \(O Z R Q\) nội tiếp. Từ đó, tứ giác \(O B Z Q\) nội tiếp. Tương tự, ta cung có tứ giác \(O C Y Q\) nội tiếp.
Xét tứ giác \(B Z Y C\) nội tiếp đường tròn \((O)\), có đường tròn \((O B Z)\) cắt đường tròn \((O C Y)\) tại điểm \(Q\), mà hai đường thẳng \(B Y\) và \(C Z\) cắt nhau tại điểm \(P\), nên \(\angle P Q O=90^{\circ}\). Từ đó \(P Q \| J T\). Mà \(J\) là trung điểm của đoạn thẳng \(A Q\) nên đường thẳng \(J T\) đi qua trung điểm của đoạn thẳng \(A P\).