Bài 1
(7 điểm)
Cho tam giác nhọn không cân \(A B C\) có các dường cao \(A D, B E, C F\) với \(D \in B C, E \in C A\) và \(F \in A B\). Gọi \(H, O\) và \(I\) tương ứng là trực tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp của tam giác \(A B C, M, N\) và \(P\) tương ứng là trung điểm các đoạn thẳng \(B C, C A\) và \(A B\). Gọi \(X, Y\) và \(Z\) tương ứng là giao điềm của các cặp đường thẳng \((A I, N P),(B I, P M)\) và \((C I, M N)\).
a) Chứng minh rằng các đường tròn ngoại tiếp các tam giác \(A X D, B Y E, C Z F\) có hai điểm chung nằm trên đường thằng OH .
b) Các đường thẳng \(X P, Y M\) và \(Z N\) tương ứng cắt lại các đường tròn ngoại tiếp các tam giác \(A X D, B Y E\) và \(C Z F\) tại các điểm \(X^{\prime}, Y^{\prime}\) và \(Z^{\prime}\left(X^{\prime} \neq X, Y^{\prime} \neq Y, Z^{\prime} \neq Z\right)\). Gọi \(J\) là điểm đối xưng của \(I\) qua \(O\). Chứng minh rằng \(X^{\prime}, Y^{\prime}\) và \(Z^{\prime}\) cùng nằm trên một đường thẳng vuông góc với đường thẳng \(H J\).
Cách giải 1:
1. Gọi \(R\) là bán kính đường tròn \((A B C)\). Ta có: \(\angle I A D=\angle X A D=\angle X D A=\angle O A I\) dẫn đển: \(O A\) tiếp xúc \((A X D)\). Suy ra phương tích từ \(O\) đến \((A X D)\) là \(R^2\). Chứng minh tương tự ta có: phương tích từ \(O\) đến \((B Y E),(C Z F)\) bằng \(R^2\).
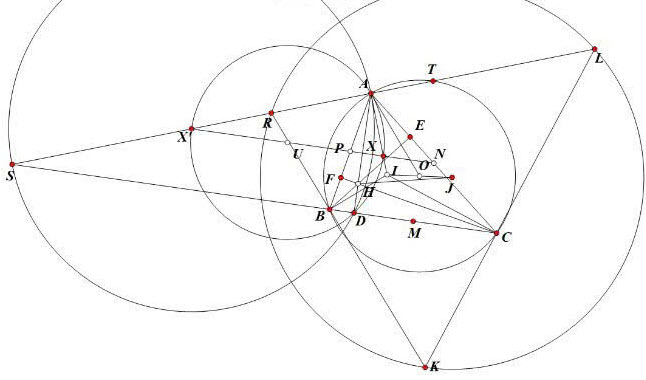
Để ý rằng: \(H A \cdot H D=H E \cdot H B=H F \cdot H C\) do đó \(H\) cùng phương tích đến ba đường tròn (AXD), (BYE), (CZF).
Từ đó suy ra: OH là trục đẳng phương của cả ba đường tròn \((A X D),(B Y E),(C Z F)\) suy ra điều phải chứng minh.
2. Gọi tâm của \((A X D),(B Y E),(C Z F)\) lần lượt là \(U, V, W\). Ta có: \(X X^{\prime}\) chính là trung trực \(A D\) dẫn đến: \(X X^{\prime}\) là đường kính của \((U)\). Gọi \(K, L, R\) lần lượt là tâm bàng góc \(A, B, C\) của tam giác \(A B C\). Ta có: \(I\) là trực tâm tam giác \(K L R\). \(O\) là tâm Euler của tam giác \(K L R\) dẫn dến: \(J\) là tâm \((K L R)\). Gọi \(A R\) cắt lại \((O)\) tại \(T\) khác \(A\) và \(A R\) cắt \(B C\) tại \(S\). Ta có: \(X^{\prime}\) là trung diểm \(A S\). Ta có: \(T\) là trung diểm \(L R\). Ta dể thấy rằng có: \(H\) thuộc trục đẳng phương của \(\left(X^{\prime} ; X^{\prime} A\right),\left(Y^{\prime} ; Y^{\prime} B\right),\left(Z ; Z^{\prime} C\right)\).
Theo hàng điểm điều hò̀ cơ bản thì: \((S A, R L)=-1\) dẫn đến: \((A S)\) hay \(\left(X^{\prime} ; X^{\prime} A\right)\) trực giao đường trờn \((K R L)\) dẫn đến phương tích từ \(J\) đến \((A S)\) bằng bán kính của \((K R L)\) bình phương.
Tương tự ta cũng có: \(J\) cùng phương tích đến \(\left(Y^{\prime} ; Y^{\prime} B\right),\left(Z^{\prime} ; Z^{\prime} C\right)\) cùng bằng bán kính của ( \(K R L\) ) bình phương.
Vậy \(X^{\prime}, Y^{\prime}, Z^{\prime}\) thẳng hàng và vuông góc \(J H\) (là trục đẳng phương của \(\left.\left(X^{\prime}\right),\left(Y^{\prime}\right),\left(Z^{\prime}\right)\right)\).
Bình luận. Bài toán khá nhẹ nhàng, có nhiều tính chất có thể đăo sâu thêm. Đã từng có các bài toán xuất hiện với ý tưởng tương tự.
Một số bài toán liên quan.
1. Cho tam giác \(A B C\) nội tiếp \((O)\) có các đường cao \(B E, C F\) cắt nhau tại \(H\). Tiếp tuyến tại \(B, C\) của \((O)\) cắt nhau tại \(P\). Đường thẳng đối xứng \(O H\) qua \(B C\) cắt đường thẳng qua \(P\) vuông góc \(E F\) tại \(K\). Lấy \(J\) đối xứng \(P\) qua \(K\). Gọi \(L\) là điểm Lemoine của tam giác \(A B C\). Chứng minh rằng \(L J\) chia đôi \(O H\).
2. (Chọn đội tuyển Ninh Bình 2024) Cho tam giác \(A B C\) nhọn, không cằn nội tiếp đường tròn \((O)\) có các đường cao \(A D, B E, C F\) dồng quy tại \(H\). Gọi \(T\) là giao điểm thứ hai của đường thẳng \(C H\) với đường tròn \((O) ; I\) là giao điểm của \(A T\) với \(B C\); \(J\) là giao điểm của \(A D\) với \(E F\). Gọi \(M, N\) lần lự̛̣t là trung điểm của các đoạn \(H C, H E\). Lấy điểm \(P\) trên \(E F\) sao cho \(M P\) song song với \(D E\), điểm \(Q\) trên \(B . J\) sao cho \(E Q\) song song với \(N P\).
a) Chứng minh rằng ba điểm \(I, E, Q\) thẳng hàng.
b) Gọi \(X\) là giao điểm cúa BH với \(\mathrm{CO}, Y\) là giao điểm của CH với \(\mathrm{BO}, Z\) là trực tâm tam giác \(D E F\). Chứng minh rằng \(O Z\) chia đôi đoạn \(X Y\).
3. Cho tam giác \(A B C\) nhọn, không cân nội tiếp \((O)\) có các đường cao \(A D, B E, C F\) cắt nhau tại \(H\). \(L\) là diểm Lemoine. Chứng minh rằng: \(O L\) di qua trực tâm tam giác \(D E F\).
Bài 2
(7 điểm)
Cho một bảng ô vuông \(3 k \times 3 k\) ( \(k\) là số nguyên dương), các ô của bảng được đánh tọa độ theo cột và hàng: ô \((i ; j)\) nằm trên cột thứ \(i\) từ trái qua phải và trên hàng thứ \(j\) từ dưới lên trên. Người ta muốn đặt \(4 k\) viên bi vào các ô của bảng, mỗi ô có không quá một viên, thỏa mãn đồng thời hai điều kiện sau:
- Mỗi hàng và mỗi cột đều có ít nhất một viên bi;
- Mỗi viên bi nằm cùng hàng hoặc cùng cột với ít nhất một viên bi khác.
a) Xét \(k=1\). Có bao nhiêu cách đặt 4 viên bi vào bảng thỏa mãn các điều kiện trên?
(Hai cách đặt bi được coi là khác nhau nếu có một ô \((i ; j)\) có bi trong một cách đặt nhưng không có bi trong cách còn lại.)
b) Xét \(k \geq 1\) tổng quát. Xác đạnh số tự nhiên \(N\) lớn nhất sao cho với mọi cách đánh đấu \(N\) ô phân biệt trên bảng, luôn tồn tại một cách đặt \(4 k\) viên bi thỏa mãn các điều kiện trên mà không có viên bi nào đặt ở một trong \(N\) ô đã được đánh dấu.
Cách giải 1:
a) Bảng 3x3 điền 4 viên bi thì dễ nhất liệt kê, xét một vài trường hợp là xong.
b) Dự đoán: N max=3k-1, vì nếu N>=3k thì chỉ cần đánh dấu 3k ô theo 1 cột là không thể xếp bi thỏa mãn yêu cầu.
Để chứng minh N=3k-1 thỏa mãn, mình nghĩ đến quy nạp và dựa trên nhận xét khá hiển nhiên sau:
Bài toán không ảnh hưởng gì nếu ta thao tác đổi chỗ các hàng, các cột.
Với k=1 và N=2, đánh dấu 2 ô tùy ý ta đều có thể đổi chỗ hàng, cột để đưa 2 ô này về trong 1 bảng con 2x2. Khi này Xếp 4 bi xung quanh bảng con 2x2 này là xong (2 bi 1 hàng, 2 bi 1 cột). Với k tổng quát, ý tưởng ta cần chọn ra một bảng con 3x3, xếp được 4 bi thỏa mãn yêu cầu, xóa 3 hàng, 3 cột của bảng con này đi và đẩy về trường hợp k-1. Với ý tưởng như vậy, ta cần chọn ra bảng con 3x3 thỏa mãn:
+ Trong bảng con chỉ có tối đa 2 ô được đánh dấu.
+ Trong 3 hàng và 3 cột của bảng con này phải chứa >=3 ô được đánh dấu.
Xét k bảng con 3x3 trên cùng 3 cột ngoài cùng bên trái, ta xét 2 TH sau:
Trường hợp 1: Trong 3 cột này chứa >=3 ô được đánh dấu, vì tổng thế có <=3k-1 ô được đánh dấu nên theo Dirichlet, tồn tại một bảng con 3x3 chứa <=2 ô đánh dấu. Thỏa mãn yêu cầu ta vừa đặt ra.
Trường hợp 2: Trong 3 cột này chứa <=2 ô được đánh dấu, khi này xét theo hàng, vì có tất cả 3k-1 ô được đánh dấu nên phải tồn tại bảng con 3x3 mà 3 hàng của nó chứa >=3 ô đánh dấu. Thỏa mãn yêu cầu ta đặt ra. Đến đây theo quy nạp ta có điều phải chứng minh.
Bài 3
(6 điểm)
Cho \(a, b, c\) là các số thực không âm thỏa mãn \(a+b+c=3\). Chứng minh rằng
\[\sqrt{3 a^3+4 b c+b+c}+\sqrt{3 b^3+4 c a+c+a}+\sqrt{3 c^3+4 a b+a+b} \geq 9\]
Cách giải 1:
Đặt \(P=\sqrt{3 a^3+4 b c+b+c}+\sqrt{3 b^3+4 c a+c+a}+\sqrt{3 c^3+4 a b+a+b}\)
Áp dụng Cauchy - Schwarz, ta có \(\left(3 a^3+4 b c+b+c\right)(3 a+4 b c+b+c) \geq\left(3 a^2+4 b c+b+c\right)^2\)
\[\Rightarrow P \geq \sum_{c y c} \dfrac{3 a^2+4 b c+b+c}{\sqrt{3 a+4 b c+b+c}}=Q\]
Tiếp tục áp dụng thêm bất đẳng thức Holder :
\(Q^2 \sum_{c y c}\left[\left(3 a^2+4 b c+b+c\right)(3 a+4 b c+b+c)\right] \geq\left(\sum_{c y c} 3 a^2+4 b c+b+c\right)^3\). Nên để chứng minh bài toán, ta đi chứng minh : \(\dfrac{\left(\sum_{c y c} 3 a^2+4 b c+b+c\right)^3}{\sum_{c y c}\left[\left(3 a^2+4 b c+b+c\right)(3 a+4 b c+b+c)\right]} \geq 81\)
Đổi biến \(p=a+b+c=3\) và tồn tại t thuộc \([0 ; 1]\) sao cho : \(q=\sum_{c y c} a b=3-3 t^2, r=a b c\), biến đổi đưa (1) trở thành \(\dfrac{18\left(45 r+4 t^6-162 t^4+477 t^2-45\right)}{48 t^4-52 t^2-10 r+91} \geq 0 \Leftrightarrow 45 r+4 t^6-162 t^4+477 t^2-45 \geq 0\)
Áp dụng bổ đề \(r \geq(1-2 t)(1+t)^2\), ta cần chỉ ra \(45(1-2 t)(1+t)^2+4 t^6-162 t^4+477 t^2-45 \geq 0\) \(\Leftrightarrow t^2\left(2 t^4-81 t^2-45 t+171\right) \geq 0\) (đúng với mọi \(\mathrm{t} \in[0 ; 1]\) )
Dấu bằng xảy ra khi và chỉ khi \(\mathrm{t}=0 \Leftrightarrow \mathrm{a}=\mathrm{b}=\mathrm{c}=1\)
Cách giải 2:(Lời giải của thầy Võ Quốc Bá Cẩn)
Ta sẽ chứng minh
\[9 \sqrt{3 a^3-a+3+4 b c} \geq 9\left(a^2+2 b c\right)-\left(a^2-b c\right)(b+c)-4(2 b c-c a-a b)\]
hay
\[9 \sqrt{3 a^3-a+3+4 b c} \geq 5 a^2+12 a+10 b c-\left(a^2-b c\right)(3-a)\]
Chú ý rằng \(f(x)=9 \sqrt{3 a^3-a+3+4 x}-5 a^2-12 a-10 x-\left(a^2-x\right)(3-a)\) là hàm liên tục và lõm trên miền \([0,+\infty)\). Mà \(0 \leq b c \leq \dfrac{(3-a)^2}{4}\) nên ta có
\[f(b c) \geq \min \left\{f(0), f\left(\dfrac{(3-a)^2}{4}\right)\right\} .\]
Như vậy, để chứng minh bất đẳng thức (1), ta chỉ cần chứng minh \(f(0) \geq 0\) và \(f\left(\dfrac{(3-a)^2}{4}\right) \geq 0\).
Bất đẳng thức \(f(0) \geq 0\) tương đương với \(9 \sqrt{3 a^3-a+3} \geq a^3+2 a^2+12 a\). Bất đẳng thức này đúng vì
\[81\left(3 a^3-a+3\right)-\left(a^3+2 a^2+12 a\right)^2=(3-a)\left(a^5+7 a^4+49 a^3-48 a^2+81\right) \geq 0\]
Bất đẳng thức \(f\left(\dfrac{(3-a)^2}{4}\right) \geq 0\) tương đương với \(9 \sqrt{3 a^3+a^2-7 a+12} \geq \dfrac{3}{4}\left(a^3+9 a^2-13 a+39\right)\). Bất đẳng thức này đúng vì
\[144\left(3 a^3+a^2-7 a+12\right)-\left(a^3+9 a^2-13 a+39\right)^2=(3-a)\left(a^3+23 a^2+163 a+69\right)(a-1)^2 \geq 0\]
Như vậy, bất đẳng thức (1) được chứng minh. Thiết lập các bất đẳng thức tương tự rồi cộng lại, ta thu được ngay kết quả cần chứng minh.
Cách giải 3:Ta có \(3 a^3+4 b c+b+c=2(a^3+2 b c)+(a^3-a+3) \geq 2(a^3+2 b c)+a^2+2\)
\((6+1+2)[2(a^3+2 b c)+a^2+2] \geq (2 \sqrt{3} \sqrt{a^3+2 b c}+a+2)^2\)
Nên
\(\sqrt{3 a^3+4 b c+b+c} \geq \dfrac{2}{\sqrt{3}} \sqrt{a^3+2 b c}+\dfrac{a+2}{3}\)
Đặt P là vế phải BĐT cần chứng minh. Ta có:
\(P \geq (\dfrac{2}{\sqrt{3}} \sum_{cyc} \sqrt{a^3+2 b c})+\dfrac{1}{3}(a+b+c+6)\)
Cần chứng minh
\(Q=\sum_{cyc} \sqrt{a^3+2 b c} \geq 3 \sqrt{3}\) (1)
Ta có: \((a^3+2 b c)(a+2 b c) \geq (a^2+2 b c)^2\)
Nên \(Q = \sum_{c y c} \sqrt{a^3+2 b c} \geq \sum_{cyc} \dfrac{a^2+2 b c}{\sqrt{a+2 b c}}=R\)
Cần chứng minh \(R \geq 3 \sqrt{3}\) hay \(R^2 \geq 27\)
Theo bất đẳng thức Holder ta có:
\(\sum_{c y c}(a^2+2 b c)(a+2 b c) \cdot R \cdot R \geq (\sum_{cyc}(a^2+2 b c))^3=(a+b+c)^6\)
Nên \(R^2 \geq \dfrac{(a+b+c)^6}{\sum_{cyc}(a^2+2bc)(a+2bc)} = S\). Cần chứng minh \(S \geq 27\).
Hay \((a+b+c)^6 \geq 3(a+b+c)^2. \sum_{cyc}(a^2+2bc)(a+2bc)\)
\(\leftrightarrow 3 \sum_{cyc}(a^2+2bc)(a+2bc) \leq (a+b+c)^4\)
\(\leftrightarrow (a^3+b^3+c^3)+18 a b c+6 a b c(a+b+c)+12(a^2 b^2+b^2 c^2+c^2 a^2) \leq (a+b+c)^4\)
\(\leftrightarrow (a+b+c)(a^3+b^3+c^3)+12 a b c(a+b+c)+12(a^2 b^2+b c^2+c^2 a^2) \leq (a+b+c)^4=(a+b+c)[a^3+b^3+c^3+3(a+b)(b+c)(c+a)]\)
\(\leftrightarrow 4 (a^2b^2+b^2c^2+c^2a^2+abc(a+b+c)) \leq (a+b+c)(a+b)(b+c)(c+a) \)
\(\leftrightarrow ab(a^2+b^2-2ab) +bc(b^2+c^2-2bc) +ca(c^2+a^2-2ca) \geq 0\)
\(\leftrightarrow a b(a-b)^2+b c(b-c)^2+c a(c-a)^2 \geq 0\)
Luôn đúng nên ta có điều phải chứng minh, dấu = xảy ra khi \(a=b=c=1\)