Bài 1
(3 điểm)
1) Giải hệ phương trình
\[ \left\{\begin{array}{l} x^2+y^2-x y=1 \\ (x+2 y)\left(1+3 y^2+5 x y\right)=27 \end{array}\right. \]
2) Giải phương trình
\[ \sqrt{7 x^2+2 x+2}+|x+1|=\sqrt{6 x^2+2}+1 \]
Cách giải 1:
1) Biến đổi phương trình tương đương với
\[ \left\{\begin{array}{l} x^2+y^2-x y=1 \quad(1) \\ (x+2 y)\left(x^2+y^2-x y+3 y^2+5 x y\right)=27 \quad(2) \end{array}\right. \]
Phương trình (2) tương đương: \((x+2 y)^3=27 \rightarrow x+2 y=3 \rightarrow x=3-2 y\)
Thay vào phương trình (1) ta có
\[ (3-2 y)^2+y^2-y(3-2 y)=1 \Leftrightarrow 7 y^2-15 y+8=0 \rightarrow y=1 \text { hoặc } y=\dfrac{8}{7} \]
Vậy phương trình có nghiệm \((y=1, x=1)\) hoặc \((y=\dfrac{8}{7}, x=\dfrac{5}{7})\).
2) Phương trình tương đương với
\[ \sqrt{7 x^2+2 x+2}+\sqrt{x^2+2 x+1}=\sqrt{6 x^2+2}+1 \quad(1) \]
Nhân liên hợp hai vế ta được
\[ \dfrac{6 x^2+1}{\sqrt{7 x^2+2 x +2}-\sqrt{x^2+2 x+1}}=\dfrac{6 x^2+1}{\sqrt{6 x^2+2}-1} \]
Vậy
\[ \sqrt{7 x^2+2 x +2}-\sqrt{x^2+2 x+1} = \sqrt{6 x^2+2}-1 \quad(2) \]
Cộng hai phương trình (1), (2) thu được:
\[ 2 \sqrt{7 x^2+2 x +2}=2 \sqrt{6 x^2+2} \Leftrightarrow x^2 + 2x =0 \leftrightarrow x=0 \text { hoặc } x=-2 \]
Bài 2
(3 điểm)
1) Tim \(x, y\) nguyên thoả mãn
\[ x^3+2 y^3+2 x^2 y+y^2 x+x+2 y=3 \]
2) Với \(x, y, z\) là những số thực thoả mãn
\[ 0 \lt x \leq y \leq z \leq 3, \quad y+z \leq 5, \quad x+y+z \leq 6 \]
Chứng minh rằng
\[ x^2+y^2+z^2 \leq 14 \]
Cách giải 1:
1) Phương trình đã cho tương đương với
\[ x^2(x+2 y)+y^2(x+2 y)+x+2 y=3 \rightarrow (x+2 y)\left(x^2+y^2+1\right)=3 \]
- Trường hợp 1
\[ \left\{\begin{array}{l}x+2 y=3 \\ x^2+y^2+1=1\end{array}\right.\]
Vô nghiệm
- Trường hợp 2
\[ \left\{\begin{array}{l}x+2 y=1 \rightarrow x=1-2 y \\ x^2+y^2+1=3 \rightarrow (1-2 y)^2+y^2=2\end{array}\right.\]
\[ \leftrightarrow 5 y^2-4 y-1=0 \rightarrow y=1, y=-\frac{1}{5}(\text { Loại }) \]
Vậy phương trình có nghiệm ( \(y=1, x=-1\) )
2) Ta có bất đẳng thức cần chứng minh tương đương với
\[ x^2+y^2+z^2 \leq 1^2+2^3+3^2 \]
\[ \leftrightarrow (1-x)(1+x)+(2-y)(2+y)+(3-z)(3+z) \geq 0 \]
\[ \leftrightarrow \underbrace{(3-z)}_{\geq 0} \underbrace{[(3+z)-(2+y)]}_{\geq 0}+\underbrace{(5-y-z)}_{\geq 0} \underbrace{[(2+y)-(1+x)]}_{\geq 0}+\underbrace{(6-x-y-z)}_{\geq 0} \underbrace{(x+1) \geq 0}_{\geq 0} \]
Bất đẳng thức luôn đúng
Bài 3
(3 điểm)
Với tứ giác \(A B C D\) lồi có hai đường chéo \(A C\) và \(B D\) cắt nhau tại \(P\). Giả sử \(Q\) là giao điểm thứ hai của các đường tròn ngoại tiếp các tam giác \(P A D\) và \(P B C\).
1) Chứng minh rằng hai tam giác \(Q D B\) và \(Q A C\) đồng dạng.
2) Chứng minh rằng \(2 \dfrac{A D}{B C} \leq \dfrac{Q D}{Q C}+\dfrac{Q A}{Q B}\).
3) Gọi \(M\) là trung diểm \(C D\). Giả sử \(Q\) nằm trong tam giác \(P C D\) và \(\angle Q P D=\angle M P C\). Chứng minh rằng \(A B C D\) là hình thang.
Cách giải 1:
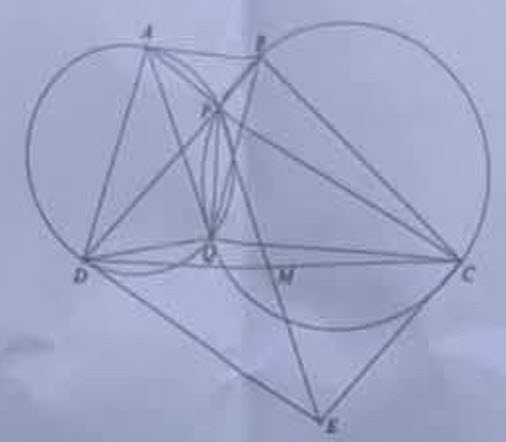
1) (1 điểm) Các tứ giác \(PQDA\) và \(PQCB\) nội tiếp nên \(\angle P D Q=\angle P A Q\) và \(\angle P B Q=\) \(\angle P C Q\). Vậy \(\triangle Q D B \sim \triangle Q A C(\mathrm{gg})\).
2) (1 điểm) Từ \(\triangle Q D B \sim \triangle Q A C\) suy ra \(\triangle Q D A \sim \triangle Q B C\) (c.g.c). Vậy
\[ 4 \frac{D A^2}{B C^2}=4 \frac{Q D}{Q B} \cdot \frac{Q A}{Q C}=4 \frac{Q D}{Q C} \cdot \frac{Q A}{Q B} \leq\left(\frac{Q D}{Q C}+\frac{Q A}{Q B}\right)^2 \]
hay
\[ 2 \dfrac{A D}{B C} \leq \dfrac{Q D}{Q C}+\dfrac{Q A}{Q B} \]
3) (1 điểm) Lấy \(E\) đối xứng \(P\) qua \(M\) thì \(P C E D\) là hình bình hành. Từ \(\angle E P C=\angle Q P D= \angle Q A D\) (giả thiết) và \(\angle P C E=\angle Q P D=\angle A Q D\) ta suy ra \(\triangle P C E \sim \triangle A Q D\) (g.g). Kết hợp 1) ta có hệ quả là
\[ \dfrac{P D}{D B}=\dfrac{E C}{D Q} \cdot \dfrac{D Q}{D B}=\dfrac{P C}{A Q} \cdot \dfrac{A Q}{A C}=\dfrac{P C}{A C} \]
Từ đẳng thức trên ta suy ra \(A B || C D\).
Bài 4
(1 điểm)
Giả sử dãy các số \(x_1, x_2, \ldots, x_n(n \geq 7)\) thoả mãn hai tính chất sau
1. Tổng của 7 số bất kỳ nhỏ hơn 15 .
2. Tổng của tất cả \(n\) số bằng 100 .
Hǎy tìm giá trị nhô nhất của n.
Cách giải 1:
- Với \(n<49\), ta chứng minh bài toán không thỏa mãn.
Giả sử phản chứng bài toán thỏa mãn, ta chia các số của dãy thành 7 nhóm, mỗi nhóm có \(\leq 7\) số. Theo giả thuyết phản chứng tổng tất cả các số \(\leq 7 * 14 = 98\) (mâu thuẫn vì tổng tất cả các số bằng 100).
- Với \(n=50\), bài toán bài toán thỏa mãn vì
\[ x_1=x_2=x_3=\cdots=x_{50}=2 \rightarrow n_{\min }=50 \]